Page 48 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

APPENDIX C

Design Examples

The design examples in Appendix C follow the AASHTO LRFD Bridge Design Specifications (BDS), 9th Edition, 2020, with proposed modifications based on the results from NCHRP Project 12-118. Further details on these proposed modifications can be found in the “Proposed AASHTO Specification Changes” document, which can be downloaded from the NCHRP Project 12-118 webpage at https://apps.trb.org/cmsfeed/TRBNetProjectDisplay.asp?ProjectID=4569.

Page 49 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Design Example 1
Simple Span Spliced Bulb-T Bridge

This design example follows the AASHTO LRFD Bridge Design Specifications (BDS), 9th Edition, 2020, with proposed modifications based on results from the NCHRP Project 12-118. Modifications to the current AASHTO BDS equations, notation, and articles are shown in Bold and/or Underlined.

195'-0" Span from CL to CL of abutments

11 - 90" Bulb T Girders labeled GA to GK spaced at 5'-9" o/c with 8" CIP composite deck

3 - Bulb T Girder segments: 31'-3", 128'-0", 31'-3" w/ 2'-0" CIP splices between girder segments and 3'-0 ⅞" CIP PT anchor block diaphragm

Precast Girder Concrete: f'ci = 7000 psi at release, f'c = 9000 psi at 28-days

CIP Splice Concrete: f'ci = 4500 psi at tendon stressing, f'c = 7250 psi at 28-days

CIP Deck Concrete: f'c = 4500 psi at 28-days

(4) 12-0.6" strand post-tensioning tendons stressed to 43.5 kip per strand (522 kip per tendon) with (2) tendons bonded and (2) tendons unbonded

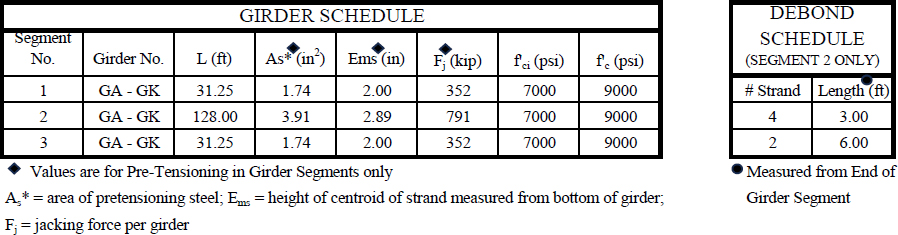
Bulb-T Girder pre-tensioning per Girder Schedule below and shown in girder cross section details.

All pre-tensioning and post-tensioning strands are 0.6" diameter 270 ksi low relaxation

Shear reinforcement is (2) #4 stirrups in the girder web spaced at 6" at the girder ends.

***Figure DE1-1: Girder and debonding schedules***

***Figure DE1-2: Superstructure section***

Page 50 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

***Figure DE1-3: Girder and post-tensioning tendon elevation***

***Figure DE1-4: Girder section composite section details and properties***

Flexure Example
Calculate Moment Capacity at Midspan

$M_{n} = A_{p s b} f_{p s b} (d_{p b} - \frac{a}{2}) + A_{p s u} f_{p s u} (d_{p u} - \frac{a}{2}) + A_{s} f_{s} (d_{s} - \frac{a}{2}) - A_{s}^{'} {f^{'}}_{s} (d_{s}^{'} - \frac{a}{2}) + α_{1} f_{c}^{'} (b - b_{w}) h_{f} (\frac{a}{2} - \frac{h_{f}}{2})$	*[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$f_{p s b} = f_{p u} (1 - k \frac{c}{d_{p b}})$	*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*

Page 51 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

$f_{p s u} = f_{p e} + 900 (\frac{d_{p u} - c}{l_{e}}) \leq f_{p y}$	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
a = β₁c	[LRFD Art. 5.6.2.2]
$ε_{t} = (d_{t} - c) \frac{.003}{c}$	[LRFD Fig. C5.6.2.1-1]

For T-section behavior:

c = \frac{A_{p s b} f_{p s b} + A_{p s u} f_{p s u} + A_{s} f_{s} - A_{s}^{'} f_{s}^{'} - α_{1} f_{c}^{'} (b - b_{w}) h_{f}}{α_{1} f_{c}^{'} β_{1} b_{w}}

[LRFD Eq. 5.6.3.1.3b-1]

For rectanglular section behavior:

c = \frac{A_{p s b} f_{p s b} + A_{p s u} f_{p s u} + A_{s} f_{s} - A_{s}^{'} f_{s}^{'}}{α_{1} f_{c}^{'} β_{1} b_{w}}

[LRFD Eq. 5.6.3.1.3b-2]

Minimum Bonded Reinforcement:

A_{bond_min} = 0.004A_ct	*[LRFD Art. 5.6.3.1.2]*
*A_ct = area of that part of cross section between the flexural tension face and centroid of gross section (in²)*	*[LRFD Art. 5.6.3.1.2]*

Section Design Information for Moment at Midspan:

f_pe =	165.5	ksi	Effective stress in prestressing steel after all instantaneous and time-dependent losses. Losses are calculated at the girder section per Art. 5.9.3.5.
f_pu =	270.0	ksi	Specified ultimate tensile strength of prestressing steel
k =	0.28		Factor for low relaxation strand
A_psb =	9.114	in²	Area of bonded prestressted reinforcement, includes pre-tensioned and post-tensioned bonded strands
A_psu =	5.208	in²	Area of unbonded prestressed reinforcement
d_pb =	93.48	in	Depth to centroid of bonded prestressing from extreme comp. fiber
d_pu =	83.25	in	Depth to centroid of unbonded prestressing from extreme comp. fiber
A_s =	0.00	in²	Area of nonprestressed tension reinforcement
f_y =	60.00	ksi	Specified minimum yield stress of A_s
d_s =	0.00	in	Depth to centroid of A_s from extreme compressive fiber
A'_s =	3.85	in²	Area of compression reinforcement (longitudinal deck reinforcement)
f'_y =	60.00	ksi	Specified minimum yield stress of A'_s
d'_s =	4.16	in	Depth to centroid of A'_s from extreme compressive fiber
l_e =	199.17	ft	Effective tendon length between anchorages. Calculated as average tendon length.
f'_{c_girder} =	9.0	ksi	Specified 28-day compressive strength of girder concrete
f'_{c_deck} =	4.5	ksi	Specified 28-day compressive strength of deck concrete
β_{1_girder} =	0.65		Stress block factor relative to neutral axis for girder concrete
α_{1_girder} =	0.85		Stress block factor for girder concrete
β_{1_deck} =	0.825		Stress block factor relative to neutral axis for deck concrete
α_{1_deck} =	0.85		Stress block factor for deck concrete
b =	69.00	in	Composite deck width

Page 52 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

b_w =	7.00	in	Girder gross web width
h_f =	8.00	in	Composite deck thickness
h =	98.00	in	Composite girder height
M_u =	19960	k-ft	Factored ultimate moment at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1

Calculate values for c, f_psu, and f_psb

Note: Iterative calculations shown for illustration. In practice, design programs and spreadsheets can be prepared with automated processes for this calculation.

Iteration #1

Assume initial value for c and iterate calcuations. Assume T-section behavior. Per Articles C5.6.2.2 and 5.6.3.2.6, utilize the lower concrete strength between the deck and girder for conservative results.

set c = 42.00 in

assume: f'_s = f'_y

Calculate f_psb and f_psu, then check c.

$\begin{array}{l} f_{p s u} = 165.5 + 900 (\frac{83.25 - 42.00}{(199.25) (12)}) \leq (0.9) (270.0) \\ f_{psu} = 181.0 ksi \end{array}$	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$\begin{matrix} f_{p s b} = 270.0 (1 - (0.28) (\frac{42.00}{93.48})) \\ f_{psb} = 236.0 ksi \end{matrix}$	*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*
$\begin{array}{l} c = \frac{(9.144) (236.0) + (5.208) (181.0) - (3.85) (60) - (0.85) (4.50) (69 - 7.0) (8.0)}{(0.85) (4.50) (0.825) (7.0)} \\ c = 43.72 in NG . Iterate Calculation . \end{array}$	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #2

Calculate values for f_psu and f_psb using previous c value, then check c.

f_psu =	180.4	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
f_psb =	234.6	ksi		*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*
c =	43.00	in	NG. Iterate Calculation.	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #3

Calculate values for f_psu and f_psb using previous c value, then check c.

f_psu =	180.7	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
f_psb =	235.2	ksi		*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*
c =	43.30	in	Within 1%. OK	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #4

Calculate final values for f_psu and f_psb using accepted c value.

f_psu =

180.5

ksi

Within 1%. OK

[LRFD Eq. 5.6.3.1.2-1 as modified by

Page 53 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

				*LRFD Art. 5.6.3.1.3b]*
f_psb =	235.0	ksi	Within 1%. OK	*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*

Check assumption: f'_s = f'_y

\frac{c}{d'_{s}} = \frac{43.30}{4.16} = 10.41 > 3. OK

[LRFD Art. 5.6.2.1]

Calculate "a", verify a > h_f, and check that Tension equals Compression

a = (0.825)(43.30)

a = 35.72 in

[LRFD Art. 5.6.2.2]

is a > h_f? Yes. T-section behavior confirmed.

T = (9.114)(235.0) + 5.208 180.5 + (0)(60)

T = 3082 kip

C = (0.85)(4.50)(69 − 7.0)(8.0) + (0.85) 4.50 (7.0)(35.72) + (3.85)(60)

C = 3085 kip

Check T = C T = C within 1%. OK

Calculate nominal moment capacity M_n.

\begin{array}{l} M_{n} = (9.114) (235.0) (93.48 - \frac{35.72}{2}) + (5.208) (180.5) (83.25 - \frac{35.72}{2}) + (0) (60) (0 - \frac{35.72}{2}) - (3.85) (60) (4.16 - \frac{35.72}{2}) + (0.85) (4.50) (69 - 7.0) (8.0) (\frac{35.72}{2} - \frac{8.0}{2}) \\ M_{n} = 252, 880 k-in = 21, 070 k-ft \end{array}

[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Art. 5.6.3.1.3b]

Check if section is tension-controlled, compression controlled, or transition.

ε_tl =	0.005		Tension controlled strain limit	[LRFD Art. 5.6.2.1]
ε_cl =	0.002		Compression controlled strain limit	[LRFD Art. 5.6.2.1]
d_t =	96.00	in	Depth to extreme tension steel from the extreme compression fiber	[LRFD Fig. C5.6.2.1-1]
$\begin{array}{l} \frac{ε_{t}}{d_{t} - c} = \frac{0.003}{c} \\ ε_{t} = \frac{(0.003) (96.00 - 43.30)}{43.30} \\ ε_{t} = 0.0037 \end{array}$			Transition Section	[LRFD Fig. C5.6.2.1-1]

Calculate Moment Resistance Factor

φ_cc =	0.75	Compression-controlled resistance factor	[LRFD Art. 5.5.4.2]
φ_tc =	0.90	Tension-controlled resistance factor for sections with unbonded tendons	[LRFD Art. 5.5.4.2]

Page 54 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

\begin{array}{l} φ = φ_{c c} + (φ_{t c} - φ_{c c}) (\frac{ε_{t} - ε_{c l}}{ε_{t l} - ε_{c l}}) \\ φ = 0.75 + (0.90 - 0.75) (\frac{0.0037 - 0.002}{0.005 - 0.002}) \\ φ = 0.833 \end{array}

Linear interpolation equation

Check minimum bonded reinforcement criteria.

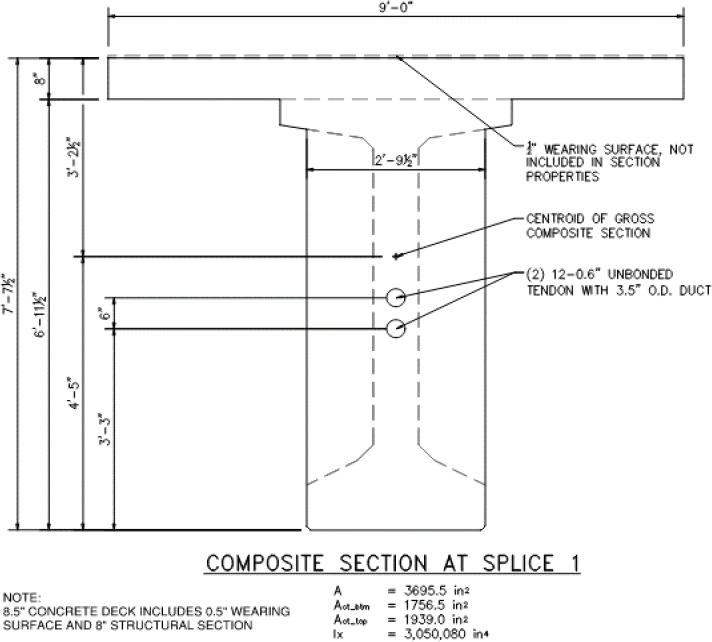
A_ct =	610.6	in²	From midspan composite section properties in Figure DE1-4	*[LRFD Art. 5.6.3.1.2]*
A_{sb_min} = A_psb =	2.442 9.114	in² in²	OK	*[LRFD Art. 5.6.3.1.2]*

Check that φ M_n ≥ M_u

φ M_n =	17,540	k-ft
M_u =	19,960	k-ft	NG!

Note that the calculated moment capacity does not include the contribution of the top flange of the precast girder in the compression block. Recalculate c and M_n while including the rectangular portion the girder top flange. Continue using f'_{c_deck} for conservatism. Alternately, the designer may use strain compatibility for a more refined estimate of flexural capacity. See Article C5.6.2.2 for more information.

Only the final iteration is shown for illustrative purposes.

set c = 27.87 in

assume: f'_s = f'_y

Calculate f_psb and f_psu, then check c.

f_psu =	186.4	ksi	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
f_psb =	247.5	ksi	*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*

\begin{array}{l} c = \frac{(9.144) (247.5) + (5.208) (186.3) - (3.85) (60) - (0.85) (4.50) [(69 - 7.0) (8.0) + (43.0 - 7.0) (3.5)]}{(0.85) (4.50) (0.825) (7.0)} \\ c = 27.87 in Within 1 % . OK \end{array}

[LRFD Eq. 5.6.3.1.3b-1]

Calculate final values for f_psu and f_psb using accepted c value.

f_psu =	186.4	ksi	Within 1%. OK	[LRFD Eq. 5.6.3.1.2-1]
f_psb =	247.5	ksi	Within 1%. OK	[LRFD Eq. 5.6.3.1.1-1]

Check assumption: f'_s = f'_y

\frac{c}{d'_{s}} =

6.70

> 3. OK

[LRFD Art. 5.6.2.1]

Calculate "a", verify a > (h_f + t_{f_girder}), and check that Tension equals Compression

Page 55 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

a =

23.00

in

[LRFD Art. 5.6.2.2]

is a > h_f + 3.5 in? Yes. T-section behavior confirmed.

T = (9.114)(247.5) + 5.208 186.4 + (0)(60)

T = 3226 kip

C = (0.85)(4.50)(69 − 7.0)(8.0) + (0.85)(4.50)(43.0 − 7.0)(3.5) + (0.85)(4.50)(7.0)(23.00) + (3.85)(60)

C = 3226 kip T = C within 1%. OK

Calculate nominal moment capacity M_n.

\begin{array}{l} M_{n} = (9.114) (247.5) (94.48 - \frac{23.00}{2}) + (5.208) (186.4) (83.25 - \frac{23.00}{2}) + (0) (60) (0 - \frac{23.00}{2}) - (3.85) (60) (4.16 - \frac{23.00}{2}) + (0.85) (4.50) [(69 - 7.0) (8.0) (\frac{23.00}{2} - \frac{8.0}{2}) + (43.0 - 7.0) (3.5) (\frac{23.00}{2} - (8.0 + \frac{3.5}{2}))] \\ M_{n} = 271, 290 k-in = 22, 610 k-ft \end{array}

[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Article 5.6.3.1.3b]

Check if section is tension-controlled, compression controlled, or transition.

ε_tl =	0.005		Tension controlled strain limit	[LRFD Art. 5.6.2.1]
ε_cl =	0.002		Compression controlled strain limit	[LRFD Art. 5.6.2.1]
d_t =	96.00	in
ε_t =	0.0073		Tension-Controlled Section	[LRFD Fig. C5.6.2.1-1]

Calculate Moment Resistance Factor

φ_comp =	0.75	Compression-controlled resistance factor	[LRFD Art. 5.5.4.2]
φ_ten =	0.90	Tension-controlled resistance factor for sections with unbonded tendons	[LRFD Art. 5.5.4.2]
φ =	0.900

Check minimum bonded reinforcement criteria.

A_ct =	610.61	in²	From midspan composite section properties in Figure DE1-4	*[LRFD Art. 5.6.3.1.2]*
A_{b_min} =	2.44	in²		*[LRFD Art. 5.6.3.1.2]*
A_psb =	9.11	in²	OK

Check that φ M_n ≥ M_u

φ M_n =	20,350 k-ft
M_u =	19,960 k-ft	OK

Shear Example
Calculate Shear Capacity at Girder End Using Sectional Design Model

V_n equals the lesser of:

V_n = V_c + V_s + V_p

[LRFD Eq. 5.7.3.3-1]

Page 56 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

V_n = 0.25f'_cb_vd_v + V_p

[LRFD Eq. 5.7.3.3-2]

where:

$V_{c} = 0.0316 β λ \sqrt{f_{c}^{'}} b_{w} d_{v}$	*[LRFD Eq. 5.7.3.3-3]*
$V_{s} = \frac{A_{v} f_{y} d_{v} (\cot θ + \cot α) \sin α}{s}$	*[LRFD Eq. 5.7.3.3-4]*

where for α = 90 degrees:

$V_{s} = \frac{A_{v} f_{y} d_{v} \cot θ}{s}$	*[LRFD Eq. C5.7.3.3-1]*
$β = \frac{4.8}{1 + 750 ε_{s}}$	[LRFD Eq. 5.7.3.4.2-1]
$θ = 29 + 3500 ε_{s}$	[LRFD Eq. 5.7.3.4.2-3]
$ε_{s} = \frac{(\frac{\| M_{u} \|}{d_{v}} + 0.5 N_{u} + \| V_{u} - V_{p} \| - A_{p s} f_{p o})}{E_{s} A_{s} + E_{p} A_{p s}}$	[LRFD Eq. 5.7.3.4.2-4]

Where:

f_po = 0.7 f_pu	appropriate for typical levels of prestressing	[LRFD Art. 5.7.3.4.2]
\|M_u\| shall not be less than: \|V_u − V_p\|d_v		[LRFD Art. 5.7.3.4.2]

Minimum Transverse Reinforcement:

A_{v} \geq 0.0316 λ \sqrt{f_{c}^{'}} \frac{b_{w} s}{f_{y}}

[LRFD Eq. 5.7.2.5-1]

Maximum Spacing of Transverse Reinforcement:

For v_u < 0.125f'_c:

s_max = 0.8d_v ≤ 24.0 in

[LRFD Eq. 5.7.2.6-1]

For v_u ≥ 0.125f'_c:

s_max = 0.4d_v ≤ 12.0 in

[LRFD Eq. 5.7.2.6-2]

Where:

$v_{u} = \frac{\| V_{u} - φ V_{p} \|}{φ b_{v} d_{v}}$	[LRFD Eq. 5.7.2.8-1]
$d_{v} = \frac{M_{n}}{A_{s} f_{y} + A_{p s b} f_{p s b} + A_{p s u} f_{p s u}}$	*[LRFD Eq. C5.7.2.8-1 as modified by LRFD Art. C5.7.2.8]*

And:

d_v ≥ greater of: 0.9d_e or 0.72h

[LRFD Art. 5.7.2.8]

in which:

Page 57 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

d_{e} = \frac{A_{p s b} f_{p s b} d_{p b} + A_{p s u} f_{p s u} d_{p u} + A_{s} f_{y} d_{s}}{A_{p s b} f_{p s b} + A_{p s u} f_{p s u} + A_{s} f_{y}}

[LRFD Eq. 5.7.2.8-2 as modified by LRFD Art. C5.7.2.8]

Section Design Information for Shear:

f_pe =	170.2	ksi	Effective stress in prestressing steel after all instantaneous and time-dependent losses calculated for this section per Art. 5.9.3.5. Note, there is less friction loss at this section relative to the midspan section used above.
f_pu =	270.0	ksi	Specified ultimate tensile strength of prestressing steel
k =	0.28		Factor for low relaxation strand
A_psb =	6.944	in²	Area of bonded prestressted reinforcement
A_psu =	5.208	in²	Area of unbonded prestressed reinforcement
d_pb =	87.98	in	Depth to centroid of bonded prestressing from extreme comp. fiber
d_pu =	52.16	in	Depth to centroid of unbonded prestressing from extreme comp. fiber
A_v =	0.40	in²	Transverse reinforcement = 2 - #4 stirrups in web
s =	6.00	in	Spacing of transverse reinforcement at section
α =	90.00	deg	Transverse reinforcement angle of inclination to longitudinal axis
A_s =	0.00	in²	Area of nonprestressed reinforcement
f_y =	60.00	ksi	Specified minimum yield stress of A_s
d_s =	0.00	in	Depth to centroid of A_s from extreme comp. fiber
A'_s =	3.85	in²	Area of compression reinforcement (longitudinal deck reinforcement)
f'_y =	60.00	ksi	Specified minimum yield stress of A'_s
d'_s =	4.16	in	Depth to centroid of A'_s from extreme comp. fiber
E_s =	29000	ksi	Modulus of elasticity of steel reinforcement
E_p =	28500	ksi	Modulus of elasticity of prestressing steel
l_e =	199.25	ft	Effective tendon length between anchorages
f'_{c_girder} =	9.00	ksi	Specified 28-day compressive strength of girder concrete
f'_{c_deck} =	4.50	ksi	Specified 28-day compressive strength of deck concrete
λ_girder =	1.00		Concrete density modification factor for girder concrete
λ_deck =	1.00		Concrete density modification factor for deck concrete
β_{1_girder} =	0.65		Stress block factor relative to neutral axis for girder concrete
α_{1_girder} =	0.85		Stress block factor for girder concrete
β_{1_deck} =	0.825		Stress block factor relative to neutral axis for deck concrete
α_{1_deck} =	0.85		Stress block factor for deck concrete
b =	69.00	in	Composite deck width
b_w =	7.00	in	Girder gross web width
b_v =	3.50	in	Girder effective web width reduced by duct diameter
d_duct =	3.50	in	PT Duct outside diameter
h_f =	8.00	in	Composite deck thickness
h =	98.00	in	Composite girder height
V_u =	448.3	kip	Factored ultimate verical shear at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1
V_p =	145.2	kip	Vertical component of post-tensioning force at section
M_u =	3070	k-ft	Factored ultimate moment at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1

Page 58 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

N_u =

-1873.5

kip

Factored axial force at section at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1 (negative indicates compression)

Calculate values of M_n, f_psb, f_psu, and d_e needed for calculation of d_v

Only final iteration shown for illustrative purposes.

Assume initial value for c and iterate calcuations. Assume T-section behavior.

Per Articles C5.6.2.2 and 5.6.3.2.6, utilize the lower concrete strength between the deck and girder for conservative results.

set c = 24.62 in

Calculate f_psb and f_psu, then check c.

f_psu =	180.6	ksi		[LRFD Eq. 5.6.3.1.2-1]
f_psb =	248.8	ksi		[LRFD Eq. 5.6.3.1.1-1]
c =	24.45	in	Within 1%. OK	*[LRFD Eq. 5.6.3.1.3b-1]*

Calculate final values for f_psu and f_psb using accepted c value.

f_psu =	180.6	ksi	Within 1%. OK	[LRFD Eq. 5.6.3.1.2-1]
f_psb =	249.0	ksi	Within 1%. OK	[LRFD Eq. 5.6.3.1.1-1]

Calculate nominal moment capacity M_n.

a =	20.17	in	a > hf, T-section behavior confirmed.	[LRFD Art. 5.6.2.2]
M_n =	185,810	k-in =	15,480 k-ft	*[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Article 5.6.3.1.3b]*

Calculate value of d_e

\begin{array}{l} d_{e} = \frac{(6.944) (249.0) (87.98) + (5.208) (180.6) (52.16)}{(6.944) (249.1) + (5.208) (180.9)} \\ d_{e} = 75.36 in \end{array}

[LRFD Eq. 5.7.2.8-2 as modified by LRFD Art. C5.7.2.8]

Calculate value of d_v

\begin{array}{l} d_{v} = \frac{185, 810}{(6.944) (249.0) + (5.208) (180.6)} \\ d_{v} = 69.60 in \end{array}

[LRFD Eq. C5.7.2.8-1 as modified by LRFD Art. C5.7.2.8]

but not lesser than the greater of:

0.9d_e = (0.9)(75.36) =	67.82 in	[LRFD Art. 5.7.2.8]
	or
0.72h = (0.72)(98) =	70.56 in	[LRFD Art. 5.7.2.8]
d_v = 70.56 in	Final value of d_v

Calculate values of β and θ needed for calculation of V_c and V_s.

Page 59 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

\begin{array}{l} ε_{s} = \frac{(\frac{| (3070) (12) |}{70.56} + 0.5 (- 1873.5) + | 448.3 - 145.2 | - (6.944 + 5.208) (0.7) (270))}{(28, 500) (6.944 + 5.208)} \\ ε_{s} = - 0.00695 Negative value . Use 0. \end{array}

[LRFD Eq. 5.7.3.4.2-4]

Check M_u ≥ |V_u-V_p|d_v

|V_u − V_p|d_v = |448.3 − 145.2|(70.56) =

= 21,387 k-in OK

[LRFD Art. 5.7.3.4.2]

$\begin{array}{r} β = \frac{4.8}{1 + 750 (0)} \\ β = 4.8 \end{array}$	[LRFD Eq. 5.7.3.4.2-1]
θ = 29 + 3500(0) θ = 29	[LRFD Eq. 5.7.3.4.2-3]

Calculate values of V_c and V_s.

$V_{c} = (0.0316) (4.8) (1.0) \sqrt{9.00} (7.0) (70.56)$
V_c = 112.4 kip	*[LRFD Eq. 5.7.3.3-3]*

$V_{s} = \frac{(0.40) (60.0) (70.56) \cot (29)}{6.0}$
V_s = 509.2 kip		*[LRFD Eq. 5.7.3.3-4]*
φ = 0.85	For shear in prestressed members having unbonded tendons.	[LRFD Art. 5.5.4.2]

Check minimum transverse reinforcement and maximum transverse reinforcement spacing.

$A_{v} \geq (0.0316) (1.0) \sqrt{9.00} \frac{(7.0) (6.0)}{(60.0)}$
A_{v_min} = 0.07 in² OK	*[LRFD Eq. 5.7.2.5-1]*
0.125f'_c = (0.125)(9.00) = 1.13 ksi	[LRFD Eq. 5.7.2.6-1] and [LRFD Eq. 5.7.2.6-2]
$\begin{array}{l} v_{u} = \frac{\| 448.3 - (0.85) (145.2) \|}{(0.85) (3.50) (70.56)} \\ v_{u} = 1.55 ksi \geq 0.125 f^{'} c \end{array}$	[LRFD Eq. 5.7.2.8-1]
s_max = 0.4(70.56) ≤ 12.0 in
s_max = 12.0 in > s, O.K.	[LRFD Eq. 5.7.2.6-2]

Calculate factored shear resistance and check against ultimate shear load.

V_n = 112.4 + 509.2 + 145.2
= 766.8 kip	[LRFD Eq. 5.7.3.3-1]

but not greater than:

V_n = 0.25(9.00)(3.50)(70.56) + 145.2
= 700.9 kip	[LRFD Eq. 5.7.3.3-2]

Page 60 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

V_n =	700.9	kip
φ V_n =	595.7	kip
V_u =	448.3	kip	< φVn, OK

Page 61 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Design Example 2
3-Span Continuous Spliced Bulb-T Bridge

This design example follows the AASHTO LRFD Bridge Design Specifications (BDS), 9th Edition, 2020, with proposed modifications based on results from the NCHRP Project 12-118. Modifications to the current AASHTO BDS equations, notation, and articles are shown in Bold and/or Underlined.

Span configuration: 123'-0" - 200'-0" - 126'-0" from CL to CL of piers along bridge CL.

Pier 3 and Pier 6 skew angle = 0.0°, Pier 4 and Pier 5 skew angle = 38.0°

4 - 83.5" Bulb T Girder lines spaced at 9'-0" o/c with 8.5" CIP composite deck (8" structural and 0.5" sacrificial)

Each girder line has a different span configuration due to the skewed interior bents. Investigate Girder Line 2.

Girder Line 2 span configuration: 119'-5 ⅞" - 200'-0" - 129'-3 ⅛"

3 - Bulb T Girder segments: 148'-6", 148'-6", 148'-6" w/ 1'-6" CIP splices between girder segments and 3'-0" Precast PT anchor block and 3'-0" thickened web transition

Precast Girder Concrete: f'ci = 6.00 ksi at release, f'c = 8.50 ksi at 28-days

CIP Splice Concrete: f'ci = 4.50 ksi at tendon stressing, f'c = 6.00 ksi at 28-days

CIP Deck Concrete: f'c = 4.00 ksi at 28-days

(2) 12-0.6" strand undbonded post-tensioning tendons with 3.5" OD duct stressed to 0.75fpu (527.3 kip per tendon)

Bridge is erected with staged construction. Center span drop-in girder segment is supported from cantiliver overhang of the end girder segments using embedded steel erection corbels.

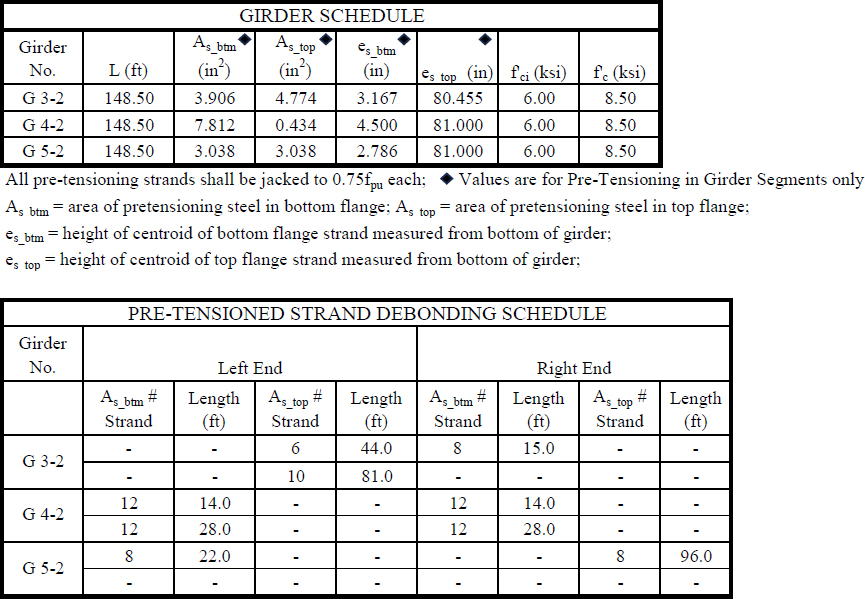
Bulb-T Girder pre-tensioning per Girder Schedule below and shown in girder cross section details.

All pre-tensioning and post-tensioning strands are 0.6" diameter 270 ksi low relaxation

***Figure DE2-1: Girder and debonding schedules***

Page 62 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

***Figure DE2-2: Superstructure section amd span layout***

Page 63 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

***Figure DE2-3: Girder Elevation, PT tendon elevation, Girder Pretensioning Details***

Page 64 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

***Figure DE2-4: Girder composite section details and properties***

Flexure Example
Check Positive and Negative Moment Capacity at Splice 1

$M_{n} = A_{p s b} f_{p s b} (d_{p b} - \frac{a}{2}) + A_{p s u} f_{p s u} (d_{p u} - \frac{a}{2}) + A_{s} f_{s} (d_{s} - \frac{a}{2}) - A_{s}^{'} {f^{'}}_{s} (d_{s}^{'} - \frac{a}{2}) + α_{1} f_{c}^{'}_{c} (b - b_{w}) h_{f} (\frac{a}{2} - \frac{h_{f}}{2})$	*[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$f_{p s b} = f_{p u} (1 - k \frac{c}{d_{p b}})$	*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*
$f_{p s u} = f_{p e} + 900 (\frac{d_{p u} - c}{l_{e}}) \leq f_{p y}$	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$a = β_{1} c$	[LRFD Art. 5.6.2.2]
$ε_{t} = (d_{t} - c) \frac{.003}{c}$	[LRFD Fig. C5.6.2.1-1]

For T-section behavior:

c = \frac{A_{p s b} f_{p s b} + A_{p s u} f_{p s u} + A_{s} f_{s} - A_{s}^{'} f_{s}^{'} - α_{1} f_{c}^{'} (b - b_{w}) h_{f}}{α_{1} f_{c}^{'} β_{1} b_{w}}

[LRFD Eq. 5.6.3.1.3b-1]

Page 65 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

For rectanglular section behavior:

c = \frac{A_{p s b} f_{p s b} + A_{p s u} f_{p s u} + A_{s} f_{s} - A_{s}^{'} f_{s}^{'}}{α_{1} f_{c}^{'} β_{1} b}

[LRFD Eq. 5.6.3.1.3b-2]

Minimum Bonded Reinforcement:

A_{bond_min} = 0.004A_ct	*[LRFD Art. 5.6.3.1.2]*
*A_ct = area of that part of cross section between the flexural tension face and centroid of gross section (in²)*	*[LRFD Art. 5.6.3.1.2]*

Section Design Information for Moment:

f_pe =	158.2	ksi	Effective stress in prestressing steel after all instantaneous and time-dependent losses. Losses are calculated at the girder section per Art. 5.9.3.5.
f_pu =	270.0	ksi	Specified ultimate tensile strength of prestressing steel
k =	0.28		Factor for low relaxation strand
A_psb =	0	in²	Area of bonded prestressed reinforcement
A_psu =	5.208	in²	Area of unbonded prestressed reinforcement
d_pb =	0.00	in	Depth to centroid of bonded prestressing from extreme comp. fiber
d_{pu_pos} =	49.50	in	Depth to centroid of unbonded prestressing from extreme comp. fiber for positive moment
d_{pu_neg} =	42.00	in	Depth to centroid of unbonded prestressing from extreme comp. fiber for negative moment
A_s =	varies	in²	Area of nonprestressed tension reinforcement, equal to A_{s_btm} for positive moment and A_{s_deck} for negative moment
A'_s =	varies	in²	Area of compression reinforcement, equal to A_{s_deck} for positive moment and A_{s_btm} for negative moment
A_{s_deck} =	5.58	in²	Area of nonprestressed reinforcement in the composite deck (#5 spaced at 6" o/c)
f_{y_deck} =	60.00	ksi	Specified minimum yield stress of A_{s_deck}
d_{s_deck} =	2.81	in	Depth to centroid of A_{s_deck} from top of composite section
A_{s_btm} =	2.64	in²	Area of nonprestressed reinforcement in the girder bottom flange (6-#6 centered at 4.5" above bottom of section)
f_{y_btm} =	60.00	ksi	Specified minimum yield stress of A_{s_btm}
d_{s_btm} =	87.00	in	Depth to centroid of A_{s_btm} from top of composite section
l_e =	449.38	ft	Effective tendon length between anchorages. Calculated as average tendon length.
f'_{c_splice} =	6.00	ksi	Specified 28-day compressive strength of CIP splice concrete
f'_{c_deck} =	4.00	ksi	Specified 28-day compressive strength of deck concrete
β_{1_splice} =	0.75		Stress block factor relative to neutral axis for girder concrete
α_{1_splice} =	0.85		Stress block factor for girder concrete
β_{1_deck} =	0.85		Stress block factor relative to neutral axis for deck concrete
α_{1_deck} =	0.85		Stress block factor for deck concrete
b =	108.00	in	Composite deck width
b_w =	33.50	in	Girder gross web width at splice
h_f =	8.00	in	Composite deck thickness
h =	91.50	in	Composite girder height
M_{u_pos} =	367	k-ft	Factored ultimate positive moment at section calculated per Strength I - V load

Page 66 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

			combinations in LRFD Table 3.4.1-1
M_{u_neg} =	-3925	k-ft	Factored ultimate negative moment at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1

Check Positive Moment Capacity

Calculate values for c and f_psu. Note that f_psb is not used because there is no bonded prestressed reinforcement at the CIP splice section.

Note: Iterative calculations shown for illustration. In practice, design programs and spreadsheets can be prepared with automated processes for this calculation.

Iteration #1

Assume initial value for c and iterate calcuations. Assume rectangular section behavior with compression in deck concrete.

set c = 4.00 in

A_{s_deck} = A'_s and A_{s_btm} = A_s

assume: f_s = f_y and f'_s = f'_y

Calculate f_psu, then check c.

$\begin{array}{l} f_{p s u} = 158.2 + 900 (\frac{49.5 - 4.00}{(449.38) (12)}) \leq (0.9) (270.0) \\ f_{psu} = 165.8 ksi \end{array}$	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$\begin{array}{l} c = \frac{(5.208) (165.8) + (2.64) (60) - (5.58) (60)}{(0.85) (4.00) (0.85) (108)} \\ c = 2.20 in NG . Iterate Calculation . \end{array}$	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #2

Calculate values for f_psu using previous c value, then check c.

f_psu =	166.1	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
c =	2.21	in	Within 1%. OK	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #3

Calculate final values for f_psu using accepted c value.

f_psu =

166.1

ksi

Within 1%. OK

[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]

Calculate "a", verify a < h_f and a > d'_s

a = (0.85)(2.18)		[LRFD Art. 5.6.2.2]
a = 1.88 in
is a < h_f?	Yes. Rectangular section behavior confirmed.
is a > d'_s?	No. Compression steel located outside compression block. Recalculate c.

Page 67 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Iteration #4 Recalculate c without compression steel.

set c = 3.26 in

A_{s_btm} = A_s

assume: f_s = f_y

Calculate f_psu, then check c.

f_psu =	165.9	ksi
c =	3.28	in	Within 1%. OK

Check assumption: f_s = f_y

\frac{c}{d_{s}} = \frac{3.25}{87.00} \leq \frac{0.003}{0.003 + ε_{c l}} = 0.038 < 0.6. OK

[LRFD Art. 5.6.2.1]

Calculate "a", verify a < h_f, and check that Tension equals Compression

a =	2.78	in		[LRFD Art. 5.6.2.2]
is a < h_f?			Yes. Rectangular section behavior confirmed.

T = (5.208)(165.9) + (2.64)(60)

T = 1022 kip

C = (0.85)(4.0)(108)(2.78)

C = 1022 kip

Check T = C T = C within 1%. OK

Calculate nominal moment capacity M_n.

M_{n} = (5.208) (165.9) (49.5 - \frac{2.78}{2}) + (2.64) (60) (87.00 - \frac{2.78}{2}) + (0.85) (4.00) (108.0 - 108.0) (8.0) (\frac{2.78}{2} - \frac{8.0}{2})

[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Art. 5.6.3.1.3b]

M_n = 55,130 k-in = 4,590 k-ft

Note: Per LRFD Art. 5.6.3.2.3, for rectangular sections b_w shall be taken as b in LRFD Eq. 5.6.3.2.2-1

Check if section is tension-controlled, compression controlled, or transition.

ε_tl =	0.005		Tension controlled strain limit	[LRFD Art. 5.6.2.1]
ε_cl =	0.002		Compression controlled strain limit	[LRFD Art. 5.6.2.1]
d_t =	89.00	in	Depth to extreme tension steel from the extreme compression fiber	[LRFD Fig. C5.6.2.1-1]
$\begin{array}{l} \frac{ε_{t}}{d_{t} - c} = \frac{0.003}{c} \\ ε_{t} = \frac{(0.003) (89.00 - 3.25)}{3.25} \\ ε_{t} = 0.0785 \end{array}$			Tension-Controlled Section	[LRFD Fig. C5.6.2.1-1]

Page 68 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Calculate Moment Resistance Factor

φ_cc =	0.75	Compression-controlled resistance factor	[LRFD Art. 5.5.4.2]
φ_tc =	0.90	Tension-controlled resistance factor for sections with unbonded tendons	[LRFD Art. 5.5.4.2]
φ =	0.900

Check minimum bonded reinforcement criteria.

A_ct =	1756.5	in²	From midspan composite section properties in Figure DE2-4	*[LRFD Art. 5.6.3.1.2]*
A_{sb_min} =	7.026	in²		*[LRFD Art. 5.6.3.1.2]*
A_{s_btm} =	2.64	in²	NG. Provide additional bonded reinforcement

add 16 #5 bars centered at 3'-3" above bottom of girder section at splice

A_{sb_prov} = 2.64 + (16)(0.31) =

7.60 ⁱⁿ²

OK

Check that φ M_n ≥ M_u

φ M_n =	4,130	k-ft
M_u =	367	k-ft	OK

Check Negative Moment Capacity

Calculate values for c and f_psu. Note that f_psb is not used because there is no bonded prestressed reinforcement at the CIP splice section.

Note: Iterative calculations shown for illustration. In practice, design programs and spreadsheets can be prepared with automated processes for this calculation.

Iteration #1

Assume initial value for c and iterate calcuations. Assume rectangular section behavior with compression in CIP splice concrete.

set c = 7.00 in

A_{s_deck} = A_s and A_{s_btm} = A'_s

assume: f_s = f_y and f'_s = f'_y

Calculate f_psu, then check c.

$\begin{array}{l} f_{p s u} = 158.2 + 900 (\frac{42.0 - 7.00}{(449.38) (12)}) \leq (0.9) (270.0) \\ f_{psu} = 164.0 ksi \end{array}$	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$\begin{array}{l} c = \frac{(5.208) (164.0) + (5.58) (60) - (2.64) (60)}{(0.85) (6.00) (0.75) (33.50)} \\ c = 8.04 in NG . Iterate Calculation . \end{array}$	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #2

Page 69 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Calculate values for f_psu using previous c value, then check c.

f_psu =	165.1	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
c =	8.09	in	Within 1%. OK	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #3

Calculate final values for f_psu using accepted c value.

f_psu =

165.1

ksi

Within 1%. OK

[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]

Calculate "a", verify a < precast girder depth and a > d'_s

a = (0.75)(8.09)

[LRFD Art. 5.6.2.2]

a = 6.07 in

is a < precast depth?

Yes. Rectangular section behavior confirmed.

d'_s = h - d_{s_btm} = 91.5 - 85.5 =	4.50 in
is a > d'_s? Yes. Compression steel located in compression block

Check assumption: f_s = f_y

\frac{c}{d_{s}} = \frac{8.09}{91.50 - 2.81} \leq \frac{0.003}{0.003 + ε_{c l}} = 0.091 < 0.6. OK

[LRFD Art. 5.6.2.1]

Check assumption: f'_s = f'_y

$\frac{c}{d'_{s}} = \frac{8.09}{4.50} = 1.80 < 3. NG$

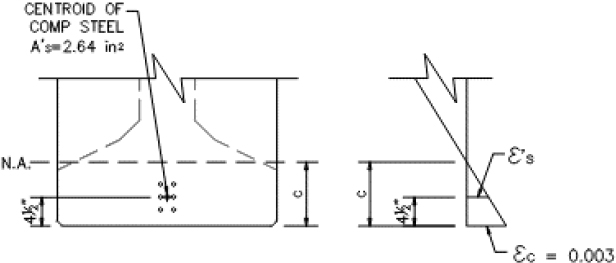
The compression steel has not yielded. Per Article 5.6.2.1 the stress in the compression steel shall be determined using strain compatibility. Alternatively, the compression steel may be ignored. For this example, calculate the stress in the compression steel using strain compatibility.

$ε'_{s} = \frac{0.003}{c} (c - 5.5 ")$
$f'_{s} = E_{s} ε'_{s}$
where: E_s = 29,000 ksi

Calculate values for c, f'_s, and f_psu. Note that f_psb is not used because there is no bonded prestressed reinforcement at the CIP splice section.

Note: Iterative calculations shown for illustration. In practice, design programs and spreadsheets can be prepared with automated processes for this calculation.

Iteration #1

Assume initial value for c and iterate calcuations. Assume rectangular section behavior with compression in CIP splice concrete. A_{s_deck} = A_s, A_{s_btm} = A'_s, and f_s = f_y

Page 70 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

set c = 8.09 in

Calculate values for f'_s and f_psu, then check c.

$\begin{array}{l} f'_{s} = (29, 000) (\frac{0.003}{8.60}) (8.6 - 4.50) \\ {f'}_{s} = 38.61 ksi \end{array}$

$\begin{array}{l} f_{p s u} = 158.2 + 900 (\frac{42.0 - 7.00}{(449.38) (12)}) \leq (0.9) (270.0) \\ f_{psu} = 163.9 ksi \end{array}$	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$\begin{array}{l} c = \frac{(5.208) (163.70) + (5.58) (60) - (2.64) (33.83)}{(0.85) (6.00) (0.75) (33.50)} \\ c = 8.48 in NG . Iterate Calculation . \end{array}$	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #2

Calculate values for f'_s and f_psu using previous c value, then check c.

f'_s =	40.82	ksi
f_psu =	165.0	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
c =	8.48	in	Within 1%. OK	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #3

Calculate final values for f'_s and f_psu using accepted c value.

f'_s =	40.83	ksi	Within 1%. OK
f_psu =	165.0	ksi	Within 1%. OK	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*

Calculate "a", verify a < precast girder depth and a > d'_s

a = 0.75 8.48
a = 6.36 in

[LRFD Art. 5.6.2.2]

	is a < precast depth?	Yes. Rectangular section behavior confirmed.
d'_s = h - d_{s_btm} = 91.5 - 87.0 =		4.50 in
	is a > d'_s?	Yes. Compression steel located in compression block

Check assumption: f_s = f_y

\frac{c}{d_{s}} = \frac{8.48}{91.50 - 2.81} \leq \frac{0.003}{0.003 + ε_{c l}} = 0.096 < 0.6. OK

[LRFD Art. 5.6.2.1]

T = (5.208)(165.0) + (5.58)(60)

T = 1194 kip

C = (0.85)(6.0)(33.50)(6.36) + (2.64)(40.83)

Page 71 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

C = 1194 kip

Check T = C

T = C within 1%. OK

Calculate nominal moment capacity M_n.

M_{n} = (5.208) (165.0) (42.0 - \frac{6.36}{2}) + (5.58) (60) (91.50 - 2.81 - \frac{6.36}{2}) - (2.64) (40.83) (4.50 - \frac{6.36}{2}) + (0.85) (6.00) (33.5 - 33.5) (8.0) (\frac{6.36}{2} - \frac{8.0}{2})

[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Art. 5.6.3.1.3b]

M_n = -61,850 k-in = -5,150 k-ft

Note: Per LRFD Art. 5.6.3.2.3, for rectangular sections bw shall be taken as b in LRFD Eq. 5.6.3.2.2-1

Check if section is tension-controlled, compression controlled, or transition.

ε_tl =	0.005		Tension controlled strain limit	[LRFD Art. 5.6.2.1]
ε_cl =	0.002		Compression controlled strain limit	[LRFD Art. 5.6.2.1]
d_t =	88.69	in	Depth to extreme tension steel from the extreme compression fiber	[LRFD Fig. C5.6.2.1-1]
$\frac{ε_{t}}{d_{t} - c} = \frac{0.003}{c}$				[LRFD Fig. C5.6.2.1-1]
$ε_{t} = \frac{(0.003) (96.00 - 43.30)}{43.30}$
ε_t =	0.0299		Tension-Controlled Section

Calculate Moment Resistance Factor

φ_cc =	0.75	Compression-controlled resistance factor	[LRFD Art. 5.5.4.2]
φ_tc =	0.90	Tension-controlled resistance factor for sections with unbonded tendons	[LRFD Art. 5.5.4.2]
φ =	0.900

Check minimum bonded reinforcement criteria.

A_ct =	1939.0	in²	From Splice 1 composite section properties in Figure DE2-4	*[LRFD Art. 5.6.3.1.2]*
A_{sb_min} =	7.756	in²		*[LRFD Art. 5.6.3.1.2]*
A_{s_deck} =	5.58	in²	NG. Provide additional bonded reinforcement

add 8 #5 bars centered at 6'-0" above bottom of girder section at splice

A_{sb_prov} = 5.58 + (8)(0.31) = 8.06 in² OK

Check that φ M_n ≥ M_u

φ M_n =	-4,640	k-ft
M_u =	-3,925	k-ft	OK

Page 72 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Shear Example
Calculate Shear Capacity at Splice 1 for Positive and Negative moment envelopes

V_n equals the lesser of:

V_n = V_c + V_s + V_p	[LRFD Eq. 5.7.3.3-1]
V_n = 0.25f'_cb_vd_v + V_p	[LRFD Eq. 5.7.3.3-2]

where:

$V_{c} = 0.0316 β λ \sqrt{f_{c}^{'}} b_{w} d_{v}$	*[LRFD Eq. 5.7.3.3-3]*
$V_{s} = \frac{A_{v} f_{y} d_{v} (\cot θ + \cot α) \sin α}{s}$	*[LRFD Eq. 5.7.3.3-4]*

where for α = 90 degrees:

$V_{s} = \frac{A_{v} f_{y} d_{v} \cot θ}{s}$	*[LRFD Eq. C5.7.3.3-1]*
$β = \frac{4.8}{1 + 750 ε_{s}}$	[LRFD Eq. 5.7.3.4.2-1]
$θ = 29 + 3500 ε_{s}$	[LRFD Eq. 5.7.3.4.2-3]
$ε_{s} = \frac{(\frac{\| M_{u} \|}{d_{v}} + 0.5 N_{u} + \| V_{u} - V_{p} \| - A_{p s} f_{p o})}{E_{s} A_{s} + E_{p} A_{p s}}$	[LRFD Eq. 5.7.3.4.2-4]

Where:

f_po = 0.7 f_pu	appropriate for typical levels of prestressing	[LRFD Art. 5.7.3.4.2]
\|M_u\| shall not be less than: \|V_u − V_p\|d_v		[LRFD Art. 5.7.3.4.2]

Minimum Transverse Reinforcement:

A_{v} \geq 0.0316 λ \sqrt{f_{c}^{'}} \frac{b_{w} s}{f_{y}}

[LRFD Eq. 5.7.2.5-1]

Maximum Spacing of Transverse Reinforcement:

$For v_{u} < 0.125 f_{c}^{'} :$
	$s_{\max} = 0.8 d_{v} \leq 24.0 i n$	[LRFD Eq. 5.7.2.6-1]
$For v_{u} < 0.125 f_{c}^{'} :$
	$s_{\max} = 0.4 d_{v} \leq 12.0 i n$	[LRFD Eq. 5.7.2.6-2]

Where:

v_{u} = \frac{| V_{u} - φ V_{p} |}{φ b_{v} d_{v}}

[LRFD Eq. 5.7.2.8-1]

Page 73 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

d_{v} = \frac{M_{n}}{A_{s} f_{y} + A_{p s b} f_{p s b} + A_{p s u} f_{p s u}}

[LRFD Eq. C5.7.2.8-1 as modified by LRFD Art. C5.7.2.8]

And:

d_v ≥ greater of: 0.9d_e or 0.72h

[LRFD Art. 5.7.2.8]

in which:

d_{e} = \frac{A_{p s b} f_{p s b} d_{p b} + A_{p s u} f_{p s u} d_{p u} + A_{s} f_{y} d_{s}}{A_{p s b} f_{p s b} + A_{p s u} f_{p s u} + A_{s} f_{y}}

[LRFD Eq. 5.7.2.8-2 as modified by LRFD Art. C5.7.2.8]

Section Design Information for Shear:

f_pe =	158.2	ksi	Effective stress in prestressing steel after all instantaneous and time-dependent losses calculated for this section per Art. 5.9.3.5.
f_pu =	270.0	ksi	Specified ultimate tensile strength of prestressing steel
k =	0.28		Factor for low relaxation strand
A_psb =	0	in²	Area of bonded prestressed reinforcement
A_psu =	5.208	in²	Area of unbonded prestressed reinforcement
d_pb =	0	in	Depth to centroid of bonded prestressing from extreme comp. fiber
d_{pu_pos} =	49.5	in	Depth to centroid of unbonded prestressing from extreme comp. fiber for positive moment
d_{pu_neg} =	42.00	in	Depth to centroid of unbonded prestressing from extreme comp. fiber for negative moment
A_v =	0.80	in²	Transverse reinforcement = 4 - #4 stirrups in web
s =	4.00	in	Spacing of transverse reinforcement at section
α =	90.00	deg	Transverse reinforcement angle of inclination to longitudinal axis
A_s =	varies	in²	Area of nonprestressed tension reinforcement, equl to A_{s_btm} for positive moment and As_deck for negative moment
A'_s =	varies	in²	Area of compression reinforcement, equl to A_{s_deck} for positive moment and A_{s_btm} for negative moment
A_{s_deck} =	5.58	in²	Area of nonprestressed reinforcement in the composite deck (#5 spaced at 6" o/c)
f_{y_deck} =	60.00	ksi	Specified minimum yield stress of A_{s_deck}
d_{s_deck} =	2.81	in	Depth to centroid of A_{s_deck} from top of composite section
A_{s_btm} =	2.64	in²	Area of nonprestressed reinforcement in the girder bottom flange (8-#5 at 4" above bottom of section)
f_{y_btm} =	60.00	ksi	Specified minimum yield stress of A_{s_btm}
d_{s_btm} =	87.00	in	Depth to centroid of A_{s_btm} from top of composite section
E_s =	29000	ksi	Modulus of elasticity of steel reinforcement
E_p =	28500	ksi	Modulus of elasticity of prestressing steel
l_e =	449.38	ft	Effective tendon length between anchorages
f'_{c_splice} =	6.00	ksi	Specified 28-day compressive strength of CIP splice concrete
f'_{c_deck} =	4.00	ksi	Specified 28-day compressive strength of deck concrete
λ_splice =	1.00		Concrete density modification factor for girder concrete
λ_deck =	1.00		Concrete density modification factor for deck concrete
β_{1_splice} =	0.75		Stress block factor relative to neutral axis for girder concrete
α_{1_splice} =	0.85		Stress block factor for girder concrete

Page 74 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

β_{1_deck} =	0.85		Stress block factor relative to neutral axis for deck concrete
α_{1_deck} =	0.85		Stress block factor for deck concrete
b =	108.00	in	Composite deck width
b_w =	33.50	in	Girder gross web width
b_v =	30.00	in	Girder effective web width reduced by duct diameter
d_duct =	3.50	in	PT Duct outside diameter
h_f =	8.00	in	Composite deck thickness
h =	91.50	in	Composite girder height
V_{u_pos} =	225.7	kip	Factored ultimate verical shear at section in positive moment envelope calculated per Strength I - V load combinations in LRFD Table 3.4.1-1
V_{u_neg} =	462.6	kip	Factored ultimate verical shear at section in negative moment envelope calculated per Strength I - V load combinations in LRFD Table 3.4.1-1
V_p =	84	kip	Vertical component of post-tensioning force at section taken as positive if resisting the applied shear
M_{u_pos} =	367	k-ft	Factored ultimate positive moment at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1
M_{u_neg} =	-3925	k-ft	Factored ultimate negative moment at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1
N_u =	-699.3	kip	Factored axial force at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1 (negative indicates compression)

Check Shear for Positive moment envelope

From the moment calcuations above the values of M_n and f_psu for positive moment are shown below.

Note that fpsb is not used because there is no bonded prestressed reinforcement at the CIP splice.

f_psu =	165.9	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
M_n =	55,130	k-in =	4,590 k-ft	*[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Article 5.6.3.1.3b]*

Calculate d_e and d_v

\begin{matrix} \begin{array}{l} d_{e} = \frac{(5.208) (165.9) (49.5) + (2.64) (60) (87.0)}{(5.208) (165.9) + (2.64) (60)} \end{array} \\ d_{e} = 55.31 in \end{matrix}

[LRFD Eq. 5.7.2.8-2 as modified by LRFD Art. C5.7.2.8]

Calculate value of d_v

\begin{array}{l} \begin{array}{l} d_{v} = \frac{55, 130}{(5.208) (165.9) + (2.64) (60)} \end{array} \\ d_{v} = 53.92 in \end{array}

[LRFD Eq. C5.7.2.8-1 as modified by LRFD Art. C5.7.2.8]

but not lesser than the greater of:

0.9d_e = (0.9)(55.31) =	48.53 in	[LRFD Art. 5.7.2.8]
	or
0.72h = (0.72)(91.50) =	65.88 in	[LRFD Art. 5.7.2.8]

Page 75 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

d_v =

65.88

in

Final value of d_v

Check M_u ≥ |V_u-V_p|d_v for positive and negative moment

|V_u − V_p|d_v = |225.7 − 84.0|(65.88) =
= 9,335 k-in >Mu, use this value

[LRFD Art. 5.7.3.4.2]

Calculate values of β and θ needed for calculation of V_c and V_s.

$\begin{matrix} ε_{s} = \frac{(\frac{\| (9, 335) \|}{65.88} + 0.5 (- 699.3) + \| 225.7 - 84.0 \| - (5.208) (0.7) (270))}{(28, 500) (5.208) + (29, 000) (2.64)} \\ ε_{s} = - 0.00467 Negative value . Use 0. \end{matrix}$	[LRFD Eq. 5.7.3.4.2-4]
$\begin{array}{r} β = \frac{4.8}{1 + 750 (0)} \\ β = 4.8 \end{array}$	[LRFD Eq. 5.7.3.4.2-1]
θ = 29 + 3500(0) θ = 29	[LRFD Eq. 5.7.3.4.2-3]

Calculate values of V_c and V_s.

$\begin{array}{l} V_{c} = (0.0316) (4.8) (1.0) \sqrt{6.00} (33.5) (65.88) \\ V_{c} = 820.0 kip \end{array}$	*[LRFD Eq. 5.7.3.3-3]*
$\begin{matrix} V_{s} = \frac{(0.80) (60.0) (65.88) \cot (29)}{4.0} \\ V_{s} = 1, 426.2 kip \end{matrix}$	*[LRFD Eq. 5.7.3.3-4]*

φ =

0.85

For shear in prestressed members having unbonded tendons.

[LRFD Art. 5.5.4.2]

Check minimum transverse reinforcement and maximum transverse reinforcement spacing.

$\begin{array}{l} A_{v} \geq (0.0316) (1.0) \sqrt{6.00} \frac{(33.5) (4.0)}{(60.0)} \\ A_{v_{-} \min} = 0.17 {in}^{2} OK \end{array}$	*[LRFD Eq. 5.7.2.5-1]*
0.125f'_c = (0.125)(6.00) = 0.75 ksi	[LRFD Eq. 5.7.2.6-1] and [LRFD Eq. 5.7.2.6-2]
$\begin{array}{l} v_{u} = \frac{\| 225.7 - (0.85) (84.0) \|}{(0.85) (30) (65.88)} \\ v_{u} = 0.09 ksi < 0.125 f'c \end{array}$	[LRFD Eq. 5.7.2.8-1]
s_max = 0.8(65.88) ≤ 24.0 in s_max = 24.0 in > s, O.K.	[LRFD Eq. 5.7.2.6-2]

Calculate factored shear resistance and check against ultimate shear load.

Page 76 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

V_n = 820.0 + 1426.2 + 84.0
= 2330.2 kip

[LRFD Eq. 5.7.3.3-1]

but not greater than:

V_n = 0.25(6.00)(30.0)(65.88) +84.0
= 3048.6 kip
V_n = 2330.2 kip

[LRFD Eq. 5.7.3.3-2]

φ V_n = 1980.7 kip

V_u = 225.7 kip < φVn, OK

Check Shear for Negative moment envelope

From moment calcuations above the values of M_n and f_psu for negative moment are shown below.

Note that fpsb is not used because there is no bonded prestressed reinforcement at the CIP splice.

f_psu =	165.0	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
M_n =	-61,850	k-in =	-5,150 k-ft	*[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Article 5.6.3.1.3b]*

Calculate d_e and d_v

\begin{array}{l} d_{e} = \frac{(5.208) (165.0) (42.0) + (5.58) (60) (91.5 - 2.81)}{(5.208) (165.1) + (5.58) (60)} \\ d_{e} = 36.41 in \end{array}

[LRFD Eq. 5.7.2.8-2 as modified by LRFD Art. C5.7.2.8]

Calculate value of d_v

\begin{array}{l} \begin{array}{l} d_{v} = \frac{61, 850}{(5.208) (165.0) + (5.58) (60)} \end{array} \\ d_{v} = 51.79 in \end{array}

[LRFD Eq. C5.7.2.8-1 as modified by LRFD Art. C5.7.2.8]

but not lesser than the greater of:

0.9d_e = (0.9)(36.42) =	32.77 in	[LRFD Art. 5.7.2.8]
	or
0.72h = (0.72)(91.50) =	65.88 in	[LRFD Art. 5.7.2.8]

d_v =

65.88

in

Final value of d_v

Check M_u ≥ |V_u-V_p|d_v for positive and negative moment

|V_u − V_p|d_v = |462.6 − 84.0|(65.88) =
= 24,942 k-in use Mu

[LRFD Art. 5.7.3.4.2]

Calculate values of β and θ needed for calculation of V_c and V_s.

$ε_{s} = \frac{(\frac{| (- 3, 925) (12) |}{65.88} + 0.5 (- 699.3) + | 462.6 - 84.0 | - (5.208) (0.7) (270))}{(28, 500) (5.208) + (29, 000) (5.58)}$

Page 77 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

ε_s = -0.00154	Negative value. Use 0.	[LRFD Eq. 5.7.3.4.2-4]
$\begin{array}{l} β = \frac{4.8}{1 + 750 (0)} \\ β = 4.8 \end{array}$		[LRFD Eq. 5.7.3.4.2-1]
θ = 29 + 3500(0) θ = 29		[LRFD Eq. 5.7.3.4.2-3]

Calculate values of V_c and V_s.

$\begin{array}{l} V_{c} = (0.0316) (4.8) (1.0) \sqrt{6.00} (33.5) (65.88) \\ V_{c} = 820.0 kip \end{array}$		*[LRFD Eq. 5.7.3.3-3]*
$\begin{array}{l} V_{s} = \frac{(0.80) (60.0) (65.88) \cot (29)}{4.0} \\ V_{s} = 1, 426.2 kip \end{array}$		*[LRFD Eq. 5.7.3.3-4]*
φ = 0.85	For shear in prestressed members having unbonded tendons.	[LRFD Art. 5.5.4.2]

Check minimum transverse reinforcement and maximum transverse reinforcement spacing.

\begin{array}{l} A_{v} \geq (0.0316) (1.0) \sqrt{6.00} \frac{(33.5) (4.0)}{(60.0)} \\ A_{v_{-} \min} = 0.17 {in}^{2} NG . Provide more transverse reinforcement . \end{array}

[LRFD Eq. 5.7.2.5-1]

0.125f'_c = (0.125)(6.00) =

0.75

ksi

[LRFD Eq. 5.7.2.6-1] and [LRFD Eq. 5.7.2.6-2]

$\begin{array}{l} v_{u} = \frac{\| 462.6 - (0.85) (84.0) \|}{(0.85) (30) (65.88)} \\ v_{u} = 0.23 ksi < 0.125 f'c \end{array}$	[LRFD Eq. 5.7.2.8-1]
s_max = 0.8(65.88) ≤ 24.0 in s_max = 24.0 in > s, O.K.	[LRFD Eq. 5.7.2.6-2]

Calculate factored shear resistance and check against ultimate shear load.

V_n = 820.0 + 1426.2 + 84.0
= 2330.2 kip

[LRFD Eq. 5.7.3.3-1]

but not greater than:

V_n = 0.25(6.00)(30.0)(65.88) +84.0
= 3048.6 kip
V_n = 2330.2 kip

[LRFD Eq. 5.7.3.3-2]

φ V_n = 1980.7 kip

V_u = 225.7 kip < φVn, OK

Page 78 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Design Example 3
3-Span Balanced Cantilever Precast Segmental Box Bridge

This design example follows the AASHTO LRFD Bridge Design Specifications (BDS), 9th Edition, 2020, with proposed modifications based on results from the NCHRP Project 12-118. Modifications to the current AASHTO BDS equations, notation, and articles are shown in Bold and/or Underlined.

Span configuration: 180'-0" - 312'-0" - 180'-0" from CL to CL of piers along bridge CL.

Variable depth double cell box girder erected using balanced cantilever method.

Precast Segment Concrete: f'ci = 4.50 ksi at release, f'c =6.50 ksi at 28-days

CIP Splice Concrete: f'ci = 4.00 ksi at tendon stressing, f'c = 6.00 ksi at 28-days

Cantilever Tendons: Tendons A - T: 11-0.6" strand PT tendons with 3.5" OD duct stressed to 0.78fpu (502.7 kip per tendon). Tendon U: 5-0.6" strand PT tendons with 2.5" OD duct stressed to 0.78fpu (228.5 kip per tendon). Cantilever tendons A to J are considered to be bonded at the completion of segment erection. Cantilever tendons K to T are considered unbonded at the completion of segment erection. All cantilever tendons are bonded for final service conditions. Refer to the most current version of PT M55.1 Specification for Grouting of Post-Tensioned Structures for time limits between stressing and grouting of tendons.

Bottom Slab Tendons: Spans 17 and 19, Tendons 2-4, 7-9, 11-13: 11-0.6" strand PT tendons with 3.5" OD duct stressed to 0.78fpu (502.7 kip per tendon).
Span 18, Tendons 1-10, 12-16: 12-0.6" strand PT tendons with 3.5" OD duct stressed to 0.78fpu (548.4 kip per tendon). All bottom slab tendons are bonded for final service conditions.

Draped Tendons: (4) 19-0.6" strand external PT tendons stressed to 0.78fpu (868.3 kip per tendon). All draped tendons are external and unbonded for final service conditions.

All post-tensioning strands are 0.6" diameter 270 ksi low relaxation

***Figure DE3-1: Segment bulk head details and tendon locations***

Page 79 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

***Figure DE3-2: Segment layout and draped tendon layout***

Page 80 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

***Figure DE3-3: Cantilever tendon layout***

Page 81 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

***Figure DE3-4: Bottom slab tendon layout***

Page 82 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Page 83 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

***Figure DE3-6: Segment section details and properties at joint 16. Cantilever tendons B - U and draped tendons are stressed at this location***

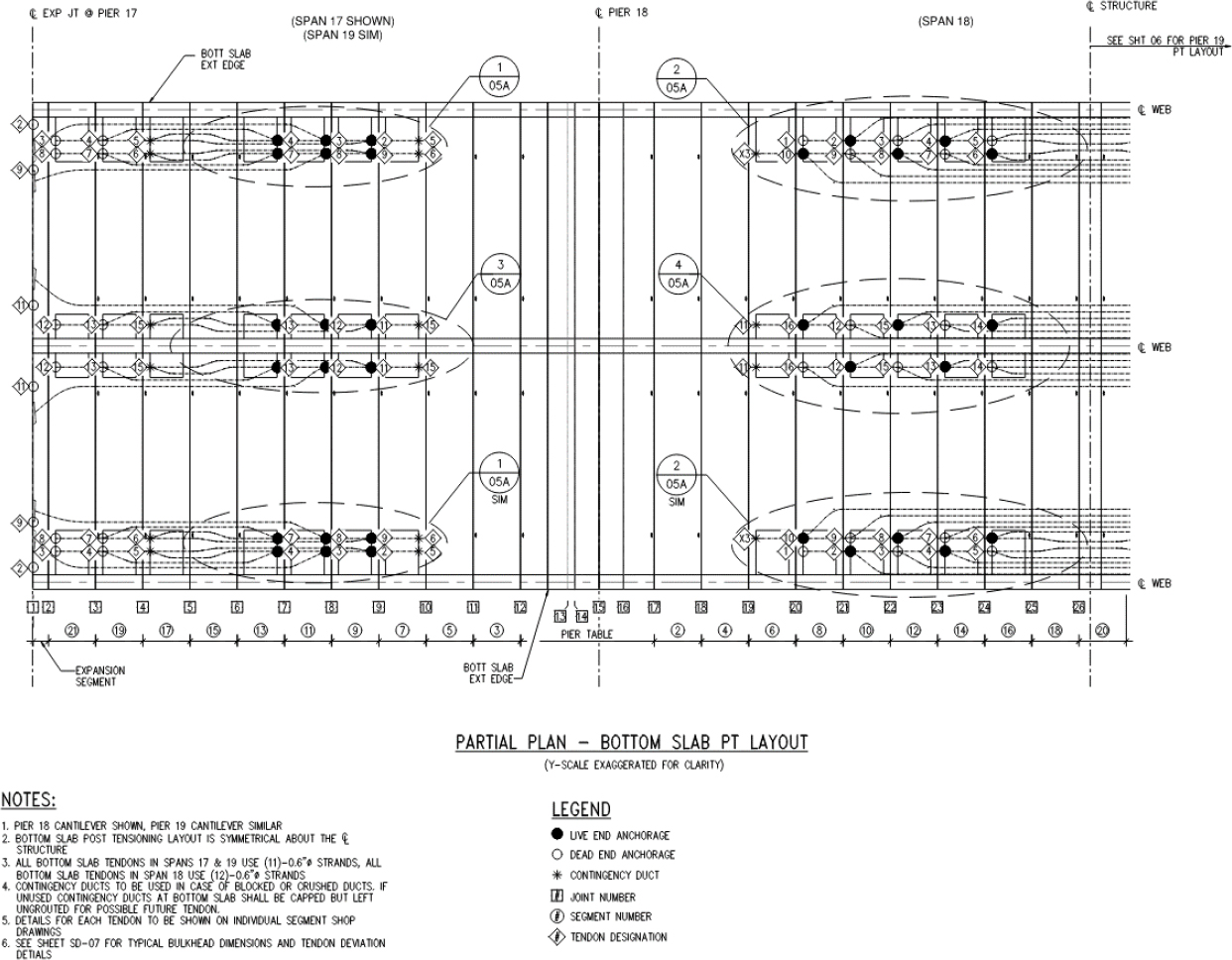
Flexure Example
Negative Moment at Joint 16 during construction and in final service

Note: At this stage all precast segments have been erected, but the closure segment has not been cast. For the purposes of this example, at this stage of construction: cantilever tendons A to J are considered to be bonded, cantilever tendons K to T are considered to be unbonded, draped tendons are installed, and Tendon U is not installed. Note that Tendon A is anchored at joint 16, and therefore is not considered to be active across the joint. Refer to the most current version of PT M55.1 Specification for Grouting of Post-Tensioned Structures for time limits between stressing and grouting of tendons.

$M_{n} = A_{p s b} f_{p s b} (d_{p b} - \frac{a}{2}) + A_{p s u} f_{p s u} (d_{p u} - \frac{a}{2}) + A_{s} f_{s} (d_{s} - \frac{a}{2}) - A_{s}^{'} {f^{'}}_{s} (d_{s}^{'} - \frac{a}{2}) + α_{1} f_{c}^{'} (b - b_{w}) h_{f} (\frac{a}{2} - \frac{h_{f}}{2})$	*[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$f_{p s b} = f_{p u} (1 - k \frac{c}{d_{p b}})$	*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*
$f_{p s u} = f_{p e} + 900 (\frac{d_{p u} - c}{l_{e}}) \leq f_{p y}$	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$a = β_{1} c$	[LRFD Art. 5.6.2.2]
$ε_{t} = (d_{t} - c) \frac{.003}{c}$	[LRFD Fig. C5.6.2.1-1]

For T-section behavior:

c = \frac{A_{p s b} f_{p s b} + A_{p s u} f_{p s u} + A_{s} f_{s} - A_{s}^{'} f_{s}^{'} - α_{1} f_{c}^{'} (b - b_{w}) h_{f}}{α_{1} f_{c}^{'} β_{1} b_{w}}

[LRFD Eq. 5.6.3.1.3b-1]

Page 84 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

For rectanglular section behavior:

c = \frac{A_{p s b} f_{p s b} + A_{p s u} f_{p s u} + A_{s} f_{s} - A_{s}^{'} f_{s}^{'}}{α_{1} f_{c}^{'} β_{1} b}

[LRFD Eq. 5.6.3.1.3b-2]

Minimum Bonded Reinforcement:

A_{bond_min} = 0.004A_ct	*[LRFD Art. 5.6.3.1.2]*
*A_ct = area of that part of cross section between the flexural tension face and centroid of gross section (in²)*	*[LRFD Art. 5.6.3.1.2]*

Section Design Information for Moment:

f_{pe_con} =	179.4	ksi	Effective stress in prestressing steel after all instantaneous and time-dependent losses during construction. Losses are calculated at section per Art. 5.9.3.5.
f_{pe_fin} =	164.3	ksi	Effective stress in prestressing steel after all instantaneous and time-dependent losses in final service. Losses are calculated at section per Art. 5.9.3.5.
f_pu =	270.0	ksi	Specified ultimate tensile strength of prestressing steel
k =	0.28		Factor for low relaxation strand
A_{psb_con} =	64.449	in²	Area of bonded prestressed negative moment reinforcement during construction
A_{psb_fin} =	138.229	in²	Area of bonded prestressed negative moment reinforcement in final service condition
A_{psu_con} =	88.102	in²	Area of unbonded prestressed negative moment reinforcement during construction
A_{psu_fin} =	16.492	in²	Area of unbonded prestressed negative moment reinforcement in final service condition
d_{pb_con} =	206.11	in	Depth to centroid of bonded negative moment prestressing from extreme compression fiber during construction
d_{pb_fin} =	207.26	in	Depth to centroid of bonded negative moment prestressing from extreme compression fiber in final service condition
d_{pu_con} =	204.23	in	Depth to centroid of unbonded negative moment prestressing from extreme compression fiber during construction
d_{pu_fin} =	187.00	in	Depth to centroid of unbonded negative moment prestressing from extreme compression fiber in final service condition
A_s =	0.00	in²	Area of nonprestressed tension reinforcement
f_y =	60.00	ksi	Specified minimum yield stress of A_s
d_s =	0.00	in	Depth to centroid of A_{s_deck} from top of section
A'_s =	0.00	in²	Area of compression reinforcement
f'_y =	60.00	ksi	Specified minimum yield stress of A'_s
d'_s =	0.00	in	Depth to centroid of A'_s from top of section
l_{e_con} =	230.54	ft	Effective tendon length between anchorages. Use average tendon length for unbonded tendons during construction stage considered.
l_{e_fin} =	193.10	ft	Effective tendon length between anchorages. Use average tendon length for unbonded tendons at final service.
f'_c =	6.50	ksi	Specified 28-day compressive strength of segment concrete
β₁ =	0.725		Stress block factor relative to neutral axis for girder concrete
α₁ =	0.85		Stress block factor for segement concrete
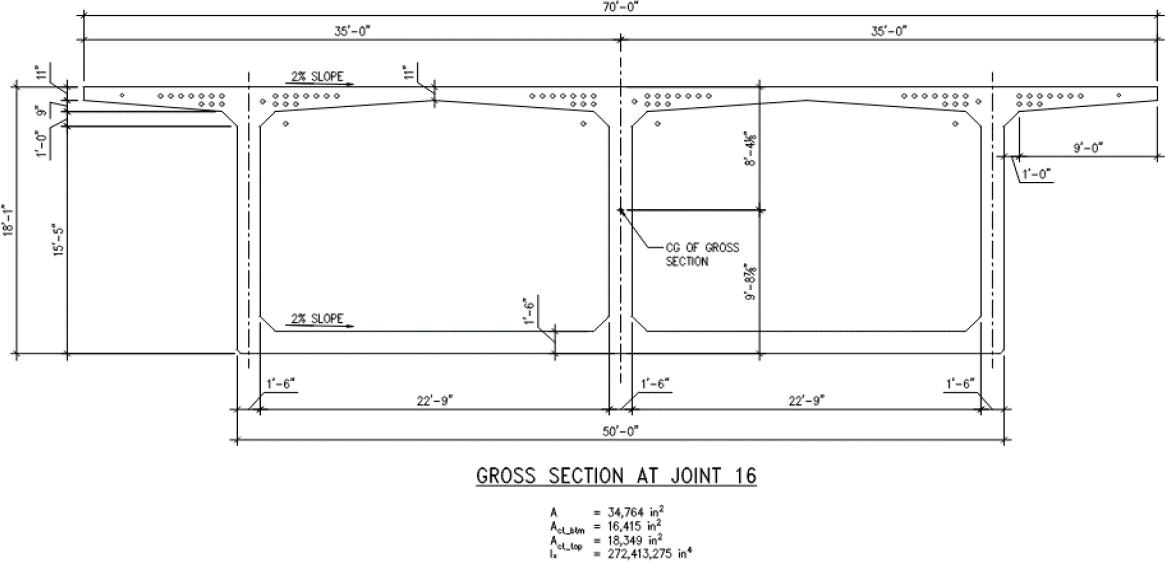
b =	600.00	in	Width of segment bottom slab
b_w =	54.00	in	Segment gross web width
h_f =	18.00	in	Thickness segment bottom slab

Page 85 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

h =	217.00	in	Segment structural section depth
M_{u_con} =	-31,935	k-ft	Factored ultimate negative moment during construction at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1
M_{u_fin} =	-349,425	k-ft	Factored ultimate negative moment in final service at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1

Check Negative Moment Capacity During Construction

Calculate values for c, f_psu, and f_psb.

Note: Iterative calculations shown for illustration. In practice, design programs and spreadsheets can be prepared with automated processes for this calculation.

Iteration #1

Assume initial value for c and iterate calcuations. Assume rectangular section behavior with compression in the segment bottom slab.

set c = 18.00 in

Calculate f_psu, then check c.

$\begin{array}{l} f_{p s u} = 179.4 + 900 (\frac{204.23 - 18.00}{(230.54) (12)}) \leq (0.9) (270.0) \\ f_{psu} = 240.0 ksi \end{array}$	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$\begin{matrix} f_{p s b} = 270 (1 - (0.28) \frac{18.0}{207.26}) \\ f_{psb} = 263.4 ksi \end{matrix}$	*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*

\begin{array}{l} c = \frac{(64.449) (263.4) + (88.102) (240.0)}{(0.85) (6.50) (0.725) (600.00)} \\ c = 15.86 in NG . Iterate Calculation . \end{array}

[LRFD Eq. 5.6.3.1.3b-1]

Iteration #2

Calculate values for f_psu using previous c value, then check c.

f_psu =	240.7	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
f_psb =	264.2	ksi		*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*
c =	15.91	in	Within 1%. OK	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #3

Calculate final values for f_psu using accepted c value.

f_psu =	240.7	ksi	Within 1%. OK	*[LRFD Eq. 5.6.3.1.2-1 as modified by*
f_psb =	264.2	ksi	Within 1%. OK	*LRFD Art. 5.6.3.1.3b]*

Calculate "a", verify a < precast girder depth and a > d'_s

a = (0.725)(15.91)
a = 11.53 in

[LRFD Art. 5.6.2.2]

Page 86 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

is a < bottom slab depth?

Yes. Rectangular section behavior confirmed.

T = (88.102)(240.7) + (64.449)(264.2)

T = 38228 kip

C = (0.85)(6.50)(600.0)(11.53)

C = 38231 kip

Check T = C T = C within 1%. OK

Calculate nominal moment capacity M_n.

M_{n} = (64.449) (264.2) (206.11 - \frac{11.53}{2}) + (88.10) (240.7) (204.23 - \frac{11.53}{2}) + (0.85) (6.00) (600.0 - 600.0) (18.0) (\frac{11.53}{2} - \frac{18.0}{2})

[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Art. 5.6.3.1.3b]

M_n = -7,619,000 k-in = -634,920 k-ft

Note: Per LRFD Art. 5.6.3.2.3, for rectangular sections b_w shall be taken as b in LRFD Eq. 5.6.3.2.2-1

Check if section is tension-controlled, compression controlled, or transition.

ε_tl =	0.005		Tension controlled strain limit	[LRFD Art. 5.6.2.1]
ε_cl =	0.002		Compression controlled strain limit	[LRFD Art. 5.6.2.1]
d_t =	209.50	in	Depth to extreme tension steel from the extreme compression fiber	[LRFD Fig. C5.6.2.1-1]
$\frac{ε_{t}}{d_{t} - c} = \frac{0.003}{c}$				[LRFD Fig. C5.6.2.1-1]
$\begin{array}{l} ε_{t} = \frac{(0.003) (96.00 - 43.30)}{43.30} \\ ε_{t} = 0.0365 \end{array}$			Tension-Controlled Section

Calculate Moment Resistance Factor

φ_cc =	0.75	Compression-controlled resistance factor	[LRFD Art. 5.5.4.2]
φ_tc =	0.90	Tension-controlled resistance factor for sections with unbonded tendons	[LRFD Art. 5.5.4.2]
φ =	0.900

Check minimum bonded reinforcement criteria.

A_ct =	18349.0	in²	From segment section properties in Figure DE3-6	*[LRFD Art. 5.6.3.1.2]*
A_{sb_min} =	73.396	in²		*[LRFD Art. 5.6.3.1.2]*
A_{psb_con} =	64.449	in²	NG. Provide additional bonded reinforcement

** Note: Tendons K thru U will be bonded prior to casting the closure pour. This is a temporary condition that occurs only under construction loading. After all cantilever tendons are bonded, the minimum reinforcement criteria will be met (this check is performed in negative moment capacity calculations for final design). Because

Page 87 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

the stress in the unbonded tendons is less than f_py non-ductile behavior may occur. Based on engineering judgement, check that φM_n ≥ 1.33M_u for construction loads at this stage.

Check that φ M_n ≥ M_u

φ M_n =	-571,430	k-ft
M_u =	-31,935	k-ft	OK

$\frac{φ M_{n}}{M_{u}} = \frac{- 571, 430}{- 31, 935} 17.89 > 1.33. OK$

Check Negative Moment Capacity for Final Design

Calculate values for c, f_psu, and f_psb.

Note: Iterative calculations shown for illustration. In practice, design programs and spreadsheets can be prepared with automated processes for this calculation.

Iteration #1

Assume initial value for c and iterate calcuations. Assume rectangular section behavior with compression in the segment bottom slab.

set c = 18.00 in

Calculate f_psu, then check c.

$\begin{array}{l} f_{p s u} = 164.3 + 900 (\frac{187.0 - 18.00}{(193.10) (12)}) \leq (0.9) (270.0) \\ f_{psu} = 229.9 ksi \end{array}$	*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
$\begin{array}{l} f_{p s b} = 270 (1 - (0.28) \frac{18.0}{207.26}) \\ f_{psb} = 263.4 ksi \end{array}$	*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*
$\begin{array}{l} c = \frac{(138.229) (263.4) + (16.492) (229.9)}{(0.85) (6.50) (0.725) (600.00)} \\ c = 16.73 in NG . Iterate Calculation . \end{array}$	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #2

Calculate values for f_psu using previous c value, then check c.

f_psu =	240.4	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
f_psb =	263.9	ksi		*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*
c =	16.83	in	Within 1%. OK	*[LRFD Eq. 5.6.3.1.3b-1]*

Iteration #3

Calculate final values for f_psu using accepted c value.

f_psu =	240.4	ksi	Within 1%. OK	*[LRFD Eq. 5.6.3.1.2-1 as modified by*
f_psb =	263.8	ksi	Within 1%. OK	*LRFD Art. 5.6.3.1.3b]*

Page 88 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Calculate "a", verify a < precast girder depth and a > d'_s

a = (0.725)(16.83)		[LRFD Art. 5.6.2.2]
a = 12.20 in
is a < bottom slab depth?	Yes. Rectangular section behavior confirmed.

T = (16.492)(240.4) + (138.229)(263.8)

T = 40433 kip

C = (0.85)(6.50)(600.00)(12.20)

C = 40438 kip

Check T = C T = C within 1%. OK

Calculate nominal moment capacity M_n.

M_{n} = (138.229) (263.8) (207.26 - \frac{12.20}{2}) + (16.492) (240.4) (187.0 - \frac{12.20}{2}) + (0.85) (6.50) (600.0 - 600.0) (18.0) (\frac{12.20}{2} - \frac{18.0}{2})

[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Art. 5.6.3.1.3b]

M_n = -8,053,060 k-in = -671,090 k-ft

Note: Per LRFD Art. 5.6.3.2.3, for rectangular sections b_w shall be taken as b in LRFD Eq. 5.6.3.2.2-1

Check if section is tension-controlled, compression controlled, or transition.

ε_tl =	0.005		Tension controlled strain limit	[LRFD Art. 5.6.2.1]
ε_cl =	0.002		Compression controlled strain limit	[LRFD Art. 5.6.2.1]
d_t =	209.50	in	Depth to extreme tension steel from the extreme compression fiber	[LRFD Fig. C5.6.2.1-1]
$\frac{ε_{t}}{d_{t} - c} = \frac{0.003}{c}$				[LRFD Fig. C5.6.2.1-1]
$\begin{array}{l} ε_{t} = \frac{(0.003) (96.00 - 43.30)}{43.30} \\ ε_{t} = 0.0344 \end{array}$			Tension-Controlled Section

Calculate Moment Resistance Factor

φ_cc =	0.75	Compression-controlled resistance factor	[LRFD Art. 5.5.4.2]
φ_tc =	0.90	Tension-controlled resistance factor for sections with unbonded tendons	[LRFD Art. 5.5.4.2]
φ =	0.900

Check minimum bonded reinforcement criteria.

A_ct =	18349.0	in²	From segment section properties in Figure DE3-5	*[LRFD Art. 5.6.3.1.2]*
A_{sb_min} =	73.396	in²		*[LRFD Art. 5.6.3.1.2]*
A_{psb_fin} =	138.23	in²	OK

Page 89 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Check that φ M_n ≥ M_u

φ M_n =	-603,980	k-ft
M_u =	-349,425	k-ft	OK

Shear Example
Calculate Shear Capacity at Joint 16 During Construction and in Final service

V_n equals the lesser of:

V_n = V_c + V_s + V_p	[LRFD Eq. 5.7.3.3-1]
V_n = 0.25f'_cb_vd_v + V_p	[LRFD Eq. 5.7.3.3-2]

where:

$V_{c} = 0.0316 β λ \sqrt{f_{c}^{'}} b_{w} d_{v}$	*[LRFD Eq. 5.7.3.3-3]*
$V_{s} = \frac{A_{v} f_{y} d_{v} (\cot θ + \cot α) \sin α}{s}$	*[LRFD Eq. 5.7.3.3-4]*

where for α = 90 degrees:

$V_{s} = \frac{A_{v} f_{y} d_{v} \cot θ}{s}$	*[LRFD Eq. C5.7.3.3-1]*
$β = \frac{4.8}{1 + 750 ε_{s}}$	[LRFD Eq. 5.7.3.4.2-1]
$θ = 29 + 3500 ε_{s}$	[LRFD Eq. 5.7.3.4.2-3]
$ε_{s} = \frac{(\frac{\| M_{u} \|}{d_{v}} + 0.5 N_{u} + \| V_{u} - V_{p} \| - A_{p s} f_{p o})}{E_{s} A_{s} + E_{p} A_{p s}}$	[LRFD Eq. 5.7.3.4.2-4]

Where:

f_po = 0.7 f_pu	appropriate for typical levels of prestressing	[LRFD Art. 5.7.3.4.2]
\|M_u\| shall not be less than: \|V_u − V_p\|d_v		[LRFD Art. 5.7.3.4.2]

Minimum Transverse Reinforcement:

A_{v} \geq 0.0316 λ \sqrt{f_{c}^{'}} \frac{b_{w} s}{f_{y}}

[LRFD Eq. 5.7.2.5-1]

Maximum Spacing of Transverse Reinforcement:

$For v_{u} < 0.125 f_{c}^{'} :$
	$s_{\max} = 0.8 d_{v} \leq 24.0 i n$	[LRFD Eq. 5.7.2.6-1]
$For v_{u} < 0.125 f_{c}^{'} :$
	$s_{\max} = 0.4 d_{v} \leq 12.0 i n$	[LRFD Eq. 5.7.2.6-2]

Where:

Page 90 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

$v_{u} = \frac{\| V_{u} - φ V_{p} \|}{φ b_{v} d_{v}}$	[LRFD Eq. 5.7.2.8-1]
$d_{v} = \frac{M_{n}}{A_{s} f_{y} + A_{p s b} f_{p s b} + A_{p s u} f_{p s u}}$	*[LRFD Eq. C5.7.2.8-1 as modified by LRFD Art. C5.7.2.8]*

And:

d_v ≥ greater of: 0.9d_e or 0.72h

[LRFD Art. 5.7.2.8]

in which:

d_{e} = \frac{A_{p s b} f_{p s b} d_{p b} + A_{p s u} f_{p s u} d_{p u} + A_{s} f_{y} d_{s}}{A_{p s b} f_{p s b} + A_{p s u} f_{p s u} + A_{s} f_{y}}

[LRFD Eq. 5.7.2.8-2 as modified by LRFD Art. C5.7.2.8]

Section Design Information for Shear:

f_{pe_con} =	179.4	ksi	Effective stress in prestressing steel after all instantaneous and time-dependent losses during construction calculated at section per Art. 5.9.3.5.
f_{pe_fin} =	164.3	ksi	Effective stress in prestressing steel after all instantaneous and time-dependent losses in final service calculated at section per Art. 5.9.3.5.
f_pu =	270.0	ksi	Specified ultimate tensile strength of prestressing steel
k =	0.28		Factor for low relaxation strand
A_{psb_con} =	64.449	in²	Area of bonded prestressed negative moment reinforcement during construction
A_{psb_fin} =	138.229	in²	Area of bonded prestressed negative moment reinforcement in final service condition
A_{psu_con} =	88.102	in²	Area of unbonded prestressed negative moment reinforcement during construction
A_{psu_fin} =	16.492	in²	Area of unbonded prestressed negative moment reinforcement in final service condition
d_{pb_con} =	206.11	in	Depth to centroid of bonded negative moment prestressing from extreme compression fiber during construction
d_{pb_fin} =	207.26	in	Depth to centroid of bonded negative moment prestressing from extreme compression fiber in final service condition
d_{pu_con} =	204.23	in	Depth to centroid of unbonded negative moment prestressing from extreme compression fiber during construction
d_{pu_fin} =	187.00	in	Depth to centroid of unbonded negative moment prestressing from extreme compression fiber in final service condition
A_v =	4.74	in²	Transverse reinforcement =6 - #8 stirrups in web
s =	6.00	in	Spacing of transverse reinforcement at section
α =	90.00	deg	Transverse reinforcement angle of inclination to longitudinal axis
A_s =	0.00	in²	Area of nonprestressed tension reinforcement
f_y =	60.00	ksi	Specified minimum yield stress of A_s
d_s =	0.00	in	Depth to centroid of A_{s_deck} from top of section
A'_s =	0.00	in²	Area of compression reinforcement
f'_y =	60.00	ksi	Specified minimum yield stress of A'_s
d'_s =	0.00	in	Depth to centroid of A'_s from top of section
E_s =	29000	ksi	Modulus of elasticity of steel reinforcement
E_p =	28500	ksi	Modulus of elasticity of prestressing steel
l_e =	230.54	ft	Effective tendon length between anchorages
f'_c =	6.50	ksi	Specified 28-day compressive strength of segment concrete

Page 91 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

λ =	1.00		Concrete density modification factor for segment concrete
β₁ =	0.725		Stress block factor relative to neutral axis for girder concrete
α₁ =	0.85		Stress block factor for segement concrete
b =	600.00	in	Width of segment bottom slab
b_w =	54.00	in	Segment gross web width
b_v =	54.00	in	Segment effective web width reduced by duct diameter
d_duct =	3.50	in	PT Duct outside diameter
h_f =	18.00	in	Thickness segment bottom slab
h =	217.00	in	Segment structural section depth
V_{u_con} =	2,892	kip	Factored ultimate verical shear at section during construction calculated per Strength I - V load combinations in LRFD Table 3.4.1-1
V_{u_fin} =	6,120	kip	Factored ultimate verical shear at section in final service calculated per Strength I - V load combinations in LRFD Table 3.4.1-1
V_p =	0	kip	Vertical component of post-tensioning force at section taken as positive if resisting the applied shear
M_{u_con} =	-31,935	k-ft	Factored ultimate negative moment during construction at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1
M_{u_fin} =	-349,425	k-ft	Factored ultimate negative moment in final service at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1
N_{u_con} =	-19,470	kip	Factored axial force during construction at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1 (negative indicates compression)
N_{u_fin} =	-18,960	kip	Factored axial force in final service at section calculated per Strength I - V load combinations in LRFD Table 3.4.1-1 (negative indicates compression)

Check Shear Capacity During Construction

From moment calcuations above the values of M_n, f_psu, and f_psb during construction are shown below.

f_psu =	240.7	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
f_psb =	264.2	ksi		*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*
M_n =	-7,619,000	k-in =	-634,920 k-ft	*[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Article 5.6.3.1.3b]*

Calculate d_e and d_v

\begin{array}{l} d_{e} = \frac{(64.449) (264.2) (206.11) + (88.102) (240.7) (204.23)}{(64.449) (264.2) + (88.102) (240.7)} \\ d_{e} = 205.07 in \end{array}

[LRFD Eq. 5.7.2.8-2 as modified by LRFD Art. C5.7.2.8]

Calculate value of d_v

\begin{array}{l} d_{v} = \frac{7, 619, 000}{(64.449) (264.2) + (88.102) (240.7)} \\ d_{v} = 199.30 in \end{array}

[LRFD Eq. C5.7.2.8-1 as modified by LRFD Art. C5.7.2.8]

but not lesser than the greater of:

Page 92 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

0.9d_e = (0.9)(205.07) =	184.56 in	[LRFD Art. 5.7.2.8]
	or
0.72h = (0.72)(217.0) =	156.24 in	[LRFD Art. 5.7.2.8]

d_v =

199.30

in

Final value of d_v

Check M_u ≥ |V_u-V_p|d_v for negative moment

|V_u − V_p|d_v = |2892 − (0)|(199.30) =
= 576,382 k-in >Mu, use this value

[LRFD Art. 5.7.3.4.2]

Calculate values of β and θ needed for calculation of V_c and V_s.

$\begin{array}{l} ε_{s} = \frac{(\frac{\| (576, 382) \|}{199.30} + 0.5 (- 19, 470) + \| 2, 892 - (0) \| - (64.449 + 88.102) (0.7) (270))}{(28500) (64.449 + 88.102)} \\ ε_{s} = - 0.00754 Negative value . Use 0. \end{array}$	[LRFD Eq. 5.7.3.4.2-4]
$\begin{array}{l} β = \frac{4.8}{1 + 750 (0)} \\ β = 4.8 \end{array}$	[LRFD Eq. 5.7.3.4.2-1]
θ = 29 + 3500(0)
θ = 29	[LRFD Eq. 5.7.3.4.2-3]

Calculate values of V_c and V_s.

$\begin{array}{l} V_{c} = (0.0316) (4.8) (1.0) \sqrt{6.50} (54.0) (199.30) \\ V_{c} = 4, 161.9 kip \end{array}$		*[LRFD Eq. 5.7.3.3-3]*
$\begin{array}{l} V_{s} = \frac{(4.74) (60.0) (199.30) \cot (29)}{6.0} \\ V_{s} = 17, 042.7 kip \end{array}$		*[LRFD Eq. 5.7.3.3-4]*
φ = 0.85	For shear in prestressed members having unbonded tendons.	[LRFD Art. 5.5.4.2]

Check minimum transverse reinforcement and maximum transverse reinforcement spacing.

$\begin{array}{l} A_{v} \geq (0.0316) (1.0) \sqrt{6.50} \frac{(54.0) (6.0)}{(60.0)} \\ A_{v_\min} = 0.44 {in}^{2} OK \end{array}$	*[LRFD Eq. 5.7.2.5-1]*
0.125f'_c = (0.125)(6.50) = 0.81 ksi	[LRFD Eq. 5.7.2.6-1] and [LRFD Eq. 5.7.2.6-2]
$\begin{array}{l} v_{u} = \frac{\| 2892 - (0.85) (0) \|}{(0.85) (54.0) (199.26)} \\ v_{u} = 0.32 ksi < 0.125 f^{'} c \end{array}$	[LRFD Eq. 5.7.2.8-1]

Page 93 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

s_max = 0.8(199.30) ≤ 24.0 in
s_max = 24.0 in > s, O.K.

[LRFD Eq. 5.7.2.6-2]

Calculate factored shear resistance and check against ultimate shear load.

V_n = 4161.9 + 17042.7 + 0
= 21204.6 kip	[LRFD Eq. 5.7.3.3-1]

but not greater than:

V_n = 0.25(6.50)(54.0)(199.26) + 0
= 17488.8 kip	[LRFD Eq. 5.7.3.3-2]
V_n = 17488.8 kip
φ V_n = 14865.5 kip
V_u = 2892.0 kip < φVn, OK

Check Shear Capacity for Final Design

From moment calcuations above the values of M_n, f_psu, and f_psb during construction are shown below.

f_psu =	240.4	ksi		*[LRFD Eq. 5.6.3.1.2-1 as modified by LRFD Art. 5.6.3.1.3b]*
f_psb =	263.9	ksi		*[LRFD Eq. 5.6.3.1.1-1 as modified by LRFD Art. 5.6.3.1.3b]*
M_n =	-8,053,060	k-in =	-671090 k-ft	*[LRFD Eq. 5.6.3.2.2-1 as modified by LRFD Article 5.6.3.1.3b]*

Calculate d_e and d_v

\begin{array}{l} d_{e} = \frac{(138.229) (263.9) (207.26) + (16.492) (240.4) (187.00)}{(138.229) (263.9) + (16.492) (240.4)} \\ d_{e} = 205.27 in \end{array}

[LRFD Eq. 5.7.2.8-2 as modified by LRFD Art. C5.7.2.8]

Calculate value of d_v

\begin{array}{l} d_{v} = \frac{8, 053, 060}{(138.229) (263.9) + (16.492) (240.4)} \\ d_{v} = 199.14 in \end{array}

[LRFD Eq. C5.7.2.8-1 as modified by LRFD Art. C5.7.2.8]

but not lesser than the greater of:

0.9d_e = (0.9)(205.27) =	184.74 in	[LRFD Art. 5.7.2.8]
	or
0.72ℎ = (0.72)(217.0) =	156.24 in	[LRFD Art. 5.7.2.8]
d_v = 199.14 in	Final value of d_v

Check M_u ≥ |V_u-V_p|d_v for positive and negative moment

\|V_u − V_p\|d_v = \|6120 − (0)\|(199.14) =				[LRFD Art. 5.7.3.4.2]
=	1,218,764	k-in	>Mu, use this value

Page 94 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.

Calculate values of β and θ needed for calculation of V_c and V_s.

$\begin{array}{l} ε_{s} = \frac{(\frac{\| (1, 218, 764) \|}{199.14} + 0.5 (- 18, 960) + \| 6, 120 - (0) \| - (138.229 + 16.492) (0.7) (270))}{(28500) (138.229 + 16.492)} \\ ε_{s} = - 0.00601 Negative value . Use 0. \end{array}$	[LRFD Eq. 5.7.3.4.2-4]
$\begin{array}{l} β = \frac{4.8}{1 + 750 (0)} \\ β = 4.8 \end{array}$	[LRFD Eq. 5.7.3.4.2-1]
θ = 29 + 3500(0)
θ = 29	[LRFD Eq. 5.7.3.4.2-3]

Calculate values of V_c and V_s.

\begin{array}{l} V_{c} = (0.0316) (4.8) (1.0) \sqrt{6.50} (54.0) (199.14) \\ V_{c} = 4, 158.6 kip \end{array}

[LRFD Eq. 5.7.3.3-3]

$\begin{array}{l} V_{s} = \frac{(4.74) (60.0) (199.14) \cot (29)}{6.0} \\ V_{s} = 17, 029.2 kip \end{array}$		*[LRFD Eq. 5.7.3.3-4]*
φ = 0.85	For shear in prestressed members having unbonded tendons.	[LRFD Art. 5.5.4.2]

Check minimum transverse reinforcement and maximum transverse reinforcement spacing.

$A_{v} \geq (0.0316) (1.0) \sqrt{6.50} \frac{(54.0) (6.0)}{(60.0)}$
A_{v_min} = 0.44 in² OK	*[LRFD Eq. 5.7.2.5-1]*
0.125f'_c = (0.125)(6.50) = 0.81 ksi	[LRFD Eq. 5.7.2.6-1] and [LRFD Eq. 5.7.2.6-2]
$v_{u} = \frac{\| 6120 - (0.85) (0) \|}{(0.85) (54.0) (199.14)}$	[LRFD Eq. 5.7.2.8-1]
v_u = 0.67 ksi < 0.125f'c
s_max = 0.4(199.14) ≤ 12.0 in
s_max = 24.0 in > s, O.K.	[LRFD Eq. 5.7.2.6-2]

Calculate factored shear resistance and check against ultimate shear load.

V_n = 4158.5 + 17028.8 + 0
= 21187.8 kip	[LRFD Eq. 5.7.3.3-1]
but not greater than:
V_n = 0.25(6.50)(54.0)(199.14) − 1652
= 17474.9 kip	[LRFD Eq. 5.7.3.3-2]

Page 95 Bookmark

Suggested Citation: "Appendix C: Design Examples." National Academies of Sciences, Engineering, and Medicine. 2025. Background and Resources for the Design and Construction of Bonded and Unbonded Post-Tensioned Concrete Bridge Elements. Washington, DC: The National Academies Press. doi: 10.17226/29032.