Appendix E

Rare-Event Species: Normal or Poisson?

This appendix provides an example of the type of analysis that can be used to identify the appropriate catch probability distribution for the purpose of catch forecasting in the case of a rare-event species. For the purpose of calculating the probability that the catch of a rare-event species will exceed a given annual catch limit (ACL), the analysis answers the question: Which is better, the normal distribution or the Poisson distribution?

THE PROBABILITY OF RARE-EVENT SPECIES CATCH: THE BINOMIAL DISTRIBUTION

In theory, the probability of catching various numbers of rare-event species fish in a specified fishery is given by the binomial distribution, and the normal distribution and Poisson distribution are just approximations to the underlying binomial distribution. This binomial distribution is discussed first, followed by discussion of the normal and Poisson distributions. To relate the binomial distribution to the catch of rare-event species in a fishery, suppose that in a given fishery, p gives the proportion of rare-event fish in the population of all fish caught in the fishery (the value of p could be estimated by the method of inverse sampling or some other method). Now in a given time period, suppose that n fish are caught in the fishery (including both rare-event and common species). The value of n is the estimated catch provided by the Marine Recreational Information Program (MRIP) (or some projection/forecast of n based on MRIP data, perhaps in combination with ancillary data). The probability that the number of rare-event fish caught, r, will be less than a prespecified ACL of rare-event fish is given by the binomial cumulative distribution function (binomial CDF) (Ross, 1988):

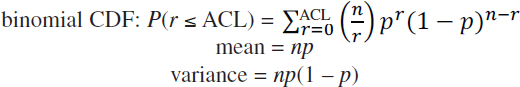
APPROXIMATIONS TO THE BINOMIAL DISTRIBUTION

Because calculating the binomial CDF can be difficult when n is very large and p is small (precisely the conditions describing the catch of a rare-event species), two probability distributions, the Poisson CDF and the normal CDF, are often used to approximate the binomial CDF (Ross, 1988).

The Poisson distribution has the advantage of being a discrete distribution, like the binomial; however, the mean and variance of the Poisson are the same, whereas the mean and the variance of the binomial are different. Another difference is that the Poisson attributes some probability to all positive values of r, regardless of the value of n, whereas the binomial attributes probability to only those positive values of r up to n.

It can be shown that, for large n, as p approaches zero, the Poisson distribution approaches the binomial distribution. Thus, the Poisson approximation improves for large n and very small p.

The normal distribution has the advantage that the mean can be different from the variance, as with the binomial; however, the normal distribution is continuous, whereas the binomial distribution is discrete. Another difference is that the normal distribution attributes some probability to all positive and negative values of r, regardless of the value of n, whereas the binomial attributes probability to only those positive values of r up to n.

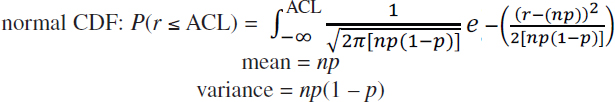
CALCULATING THE PROBABILITY OF EXCEEDING THE ACL

For each CDF, to find the probability that the catch of rare fish (r) exceeds the ACL—that is, P(r > ACL)—one simply calculates:

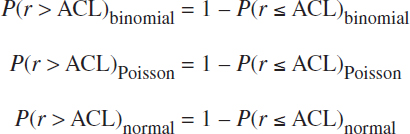
THE ERROR OF USING AN APPROXIMATION

The error associated with using either the Poisson or the normal distribution to approximate the probability of exceeding the ACL as given by the binomial distribution can be found by subtraction:

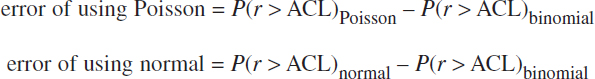
Here, a positive error measures the number of percentage points by which the approximation overestimates the probability that the catch of rare fish (r) exceeds the ACL, whereas a negative error indicates the number of percentage points by which the approximation underestimates the probability.

POISSON APPROXIMATION TO A BINOMIAL DISTRIBUTION

The binomial CDF with mean = np and variance = np(1 – p) is given by (Ross, 1988, p. 129):

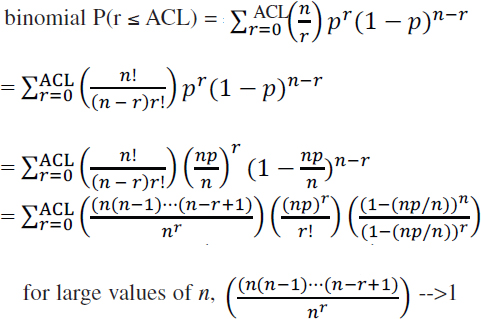
Hence, for large n:

Recall that the Poisson CDF is given by:

The error (in percentage points) of using the Poisson to approximate the binomial probability of exceeding an ACL is given by:

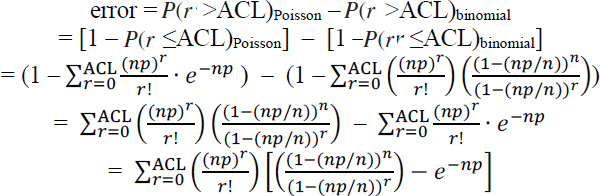
where, for large n, as p approaches zero:

Thus, for large n, as p approaches zero, the Poisson distribution approaches the binomial distribution. The Poisson is a good approximation for the binomial for large n and small p such that np is moderate in size, and np ≈ np(1 – p) (Ross, 1988, p. 129).

NORMAL APPROXIMATION TO A BINOMIAL DISTRIBUTION

The binomial CDF with mean = np and variance = np(1 – p) is given by (Ross, 1988, p. 129):

By the DeMoivre-Laplace Limit Theorem (Ross, 1988, p. 170), as n grows large, the binomial CDF P(r ≤ ACL) with mean np and variance np(1 – p) converges to the normal CDF P(r ≤ ACL + 0.5) with mean np and variance np(1 – p):

where:

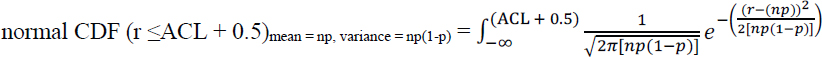
The normal distribution may not be a good approximation to the binomial distribution for values of n and p satisfying np(1 – p) < 10, that is, when the variance of the binomial distribution is less than 10 (Ross, 1988, p. 171).

The error (in percentage points) of using the normal distribution to approximate the binomial probability of exceeding an ACL is given by:

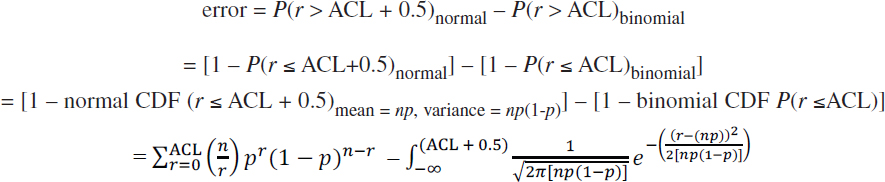
CHOOSING BETWEEN THE NORMAL AND THE POISSON

For likely values of n (e.g., estimates of n based on past catches in the fishery), an estimate of p, and a given value of the ACL for the rare-event species, the distribution (Poisson or normal) with the smaller error, as calculated above, should be used.

REFERENCE