Chapter 5. Cable Replacement

Cable replacement has been investigated in two parts in this chapter. In the first part, an optimization model was created for the traction power cables. In the second part, finite element analysis was carried out for cables. These two parts are connected since load factor plays an important role in determining the cable service life. A realistic estimation is based on a realistic model and analysis. In this chapter, a life model was created for an accurate estimation. After the optimization process, finite element analysis was carried out.

5.1. Cable Degradation Estimation for the Optimization Model

In this section, a model was introduced to determine the degree of degradation based on the actions taken at each decision epoch. Considering that the cables are tested annually, and proactive and reactive maintenance or replacement decisions are made upon the test results, it is assumed that the time between two consecutive epochs is one year. The degradation estimation model created in the research was utilized to estimate the future degradation values over the planning horizon, which may be up to 100 years. Figure 5.1 depicts the degradation process used in the research. At each decision epoch, an alternative among maintenance interventions, cable replacement, and “do nothing” was selected. Note that “do nothing” was kept until the following decision epoch in the proposed set. For simplification, two maintenance interventions were included, whereas the actual number of interventions can be different for each transport agency. The proposed model readily extends to any number of maintenance interventions.

In Figure 5.1, the current epoch is represented by t, where the current degree of degradation is observed. Assume that dt is the degree of degradation of insulated cables at the beginning of the decision epoch t. This could be estimated based on the annual test results and visual inspection. At this point, the optimization model decides on the best decision alternative among “do nothing”, replace, maintenance interventions 1 and 2. Upon the given decision, the degree of the degradation is updated, i.e., degradation is reduced via maintenance interventions and degradation is eliminated after replacement, as shown at t+δ.

5.2. Cable Failure Rate Estimation

The failure rate models can be estimated using the historical failure records. Currently, there is no such a database available for transit power cables. A national agency or organization could initiate the development of a secure online database where transit agencies can report power cable failures. Each failure record could include insulation type, jacket type, conduit, rated voltage, cable age, presence of water, exposure to extreme temperatures, underground/overhead, length of the power cable segment, the number of previous repairs on the cable, and maintenance period. Many of these factors are listed by the survey respondents: Twenty-nine mentioned water and temperature as the environmental parameters affecting the useful life of transit power cables. Furthermore, many listed jacketing and conduit as the most important physical parameters of the cable design that affect the life of transit power cables. Thus, these factors are included as potential model parameters to estimate cable failure rate. Additionally, the length of the cable segment is added to the list to normalize failure rates. Insulation and rated voltage are extensively utilized in cable failure rate models in the literature. The age of the failed cable segment is also needed for the failure models.

5.3. Process for Determining Optimal Cable Replacement Period

1. All cable failures should be collected using a secure online database to estimate cable failure rates. Each failure record should include the following information: insulation type, jacket type, conduit, rated voltage, cable age, presence of water, exposure to extreme temperatures, underground/overhead, length of the power cable segment, the number of previous repairs on the cable, maintenance period.
2. For each link on each network, if possible.
   1. Cable repair cost should be estimated (material, labor, etc.).
   2. Cable failure cost should be estimated (repair cost and cost due to loss of passengers).
   3. Cable replacement cost should be estimated (material, labor, loss of passengers, other costs).
   Otherwise, the ratio between failure and replacement costs is estimated based on historical data or expert opinion.
3. Average of optimal cost and optimal cable replacement period (T_i^*) are found by calculating the average total cost for T = 1, … , 80.
4. Identify groups of cables (two or more) that requires the closure of the same transportation lane and are in close proximity to each other. Identify the replacement cost of the group of cables. Accordingly, determine whether replacing group of cables together is cost-effective or not.

5.4. Finite Element Analysis

An efficient and accurate assessment for cables gives us better understanding in the evaluation process for cables. The Finite Element Method (FEM) is an efficient and accurate analysis tool for such assessment. This methodology was developed to identify the problems defined by partial differential equations. The three-dimensional analysis became possible with technology. Various software programs have been created using FEM. With the software, cables are modeled in layers by means of finite number of elements.

The method can be used for both linear and nonlinear analyses. The FEM involves discretization of the problem into a finite number of elements and defining equations for each element. Members are divided into meshes, and these meshes are analyzed individually. Once they are completely investigated, they are brought together to define the structural characterization of the member. The elements are assembled regarding the restraining factors and equations in the matrix form. The unknowns are identified by analyzing the equation sets. The finite numbers of elements are connected to each other by finite number of meshes. The number of unknowns for each mesh is equal to its degree of freedom. The behavior of the element is defined by the equations that involve these unknown degrees of freedom. The mathematical model of the structure is obtained by ensuring the continuity conditions on meshes.

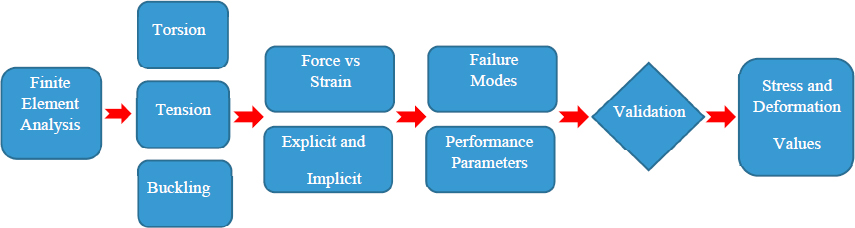
In FEM, the meshes are classified according to their geometries such as triangle, diamond, or rectangular, number of unknowns, and the characteristics of the continuum problem. They can also be categorized according to mathematical modeling due to the acquisition of the basic element matrixes. The accuracy of the FE model depends on the assumption of the meshes and the number of these meshes. Generally, the number of unknowns increases parallel to the number of meshes; hence the accuracy and certainty of the results of the analyses. Behavioral change determination was carried out under different external loads on cables. External loads were evaluated with the presented method and presented in Figure 5.2. Figure 5.3 presents stress distribution on strands under tension, torsion, and thermal loadings.

5.5. Conclusions

In this chapter, cable replacement was evaluated with optimization process and finite element analysis approach. The optimization process starts with estimating the cable failure rates. The failure rate models can be estimated using historical failure records. Each failure record should include insulation type, jacket type, conduit, rated voltage, cable age, presence of water, exposure to extreme temperatures, underground/overhead, length of the power cable segment, the number of previous repairs on the cable, and maintenance period. With such a database, cable failure rates can be estimated accurately. Then, the optimal replacement period is identified considering the cost of maintenance, replacement, and failures. In the optimization process, a period determination is very critical to determine the cable life. The procedure summarizing the determination of optimal cable replacement period. The overview of the procedure is given in Figure 5.4.

In the second part of this section, finite element analysis was carried out for the cables. Cables were analyzed under four different types of loading: Tension, Torsion, Thermal, and Water effect. With the finite element analysis, behavior of cables can be determined in various conditions. Considered conditions were among the most common conditions for the cables to investigate. With finite element analysis, cables can be modeled accurately and their conditions, environmental and physical parameters can be defined in a simulation. This simulation can be used in the decision-making process. Especially, thermal effects can be simulated through the system to assess any heat effects on cables. Continuous change in heat can be applied on the cables as a tool of monitoring system.